标签:
In the game of darts a player throws three darts at a target board which is split into twenty equal sized sections numbered one to twenty.

The score of a dart is determined by the number of the region that the dart lands in. A dart landing outside the red/green outer ring scores zero. The black and cream regions inside this ring represent single scores. However, the red/green outer ring and middle ring score double and treble scores respectively.
At the centre of the board are two concentric circles called the bull region, or bulls-eye. The outer bull is worth 25 points and the inner bull is a double, worth 50 points.
There are many variations of rules but in the most popular game the players will begin with a score 301 or 501 and the first player to reduce their running total to zero is a winner. However, it is normal to play a “doubles out” system, which means that the player must land a double (including the double bulls-eye at the centre of the board) on their final dart to win; any other dart that would reduce their running total to one or lower means the score for that set of three darts is “bust”.
When a player is able to finish on their current score it is called a “checkout” and the highest checkout is 170: T20 T20 D25 (two treble 20s and double bull).
There are exactly eleven distinct ways to checkout on a score of 6:
| D3 | ||
| D1 | D2 | |
| S2 | D2 | |
| D2 | D1 | |
| S4 | D1 | |
| S1 | S1 | D2 |
| S1 | T1 | D1 |
| S1 | S3 | D1 |
| D1 | D1 | D1 |
| D1 | S2 | D1 |
| S2 | S2 | D1 |
Note that D1 D2 is considered different to D2 D1 as they finish on different doubles. However, the combination S1 T1 D1 is considered the same as T1 S1 D1.
In addition we shall not include misses in considering combinations; for example, D3 is the same as 0 D3 and 0 0 D3.
Incredibly there are 42336 distinct ways of checking out in total.
How many distinct ways can a player checkout with a score less than 100?
在飞镖游戏中,玩家需向靶子上投掷三枚飞镖;靶子被分成了二十个相等面积的区域,并分别标上1至20。

每一枚飞镖的分数还取决于它的位置。落在外围的红/绿色圈以外时为零分,落在黑/白色区域时为一倍得分,而落在外围和中间的红/绿色圈时分别为两倍和三倍得分。
在把子的正中心有两个同心圆,被称为靶心。射中靶心外圈得25分,射中靶心内圈则得双倍50分。
飞镖的规则有许多变种,但最热门的一种是,每个玩家从301分或501分开始,轮流投掷飞镖并减去得分,首先将自己的分数减少到恰好为0的玩家获胜。不过,通常会采用“双倍结束”规则,即玩家在最后一镖必须射中一个双倍区域(包括双倍的靶心内圈)才能判定获胜。若这一轮的得分使得玩家的分数减少到1分或更少,但最后一镖未射中双倍区域,则这一轮的得分“作废”。
玩家在目前的分数下能够获胜则被称为“结分”。最高的结分为170:T20 T20 D25(两个三倍20分和一个双倍靶心)。
当玩家分数为6时,恰好有11种结分方式:
| D3 | ||
| D1 | D2 | |
| S2 | D2 | |
| D2 | D1 | |
| S4 | D1 | |
| S1 | S1 | D2 |
| S1 | T1 | D1 |
| S1 | S3 | D1 |
| D1 | D1 | D1 |
| D1 | S2 | D1 |
| S2 | S2 | D1 |
注意D1 D2被认为是不同于D2 D1的结分方式,因为它们最后的双倍不同。不过,组合S1 T1 D1和T1 S1 D1就被认为是相同的结分方式。
另外,我们在计算组合时,我们不考虑脱靶的情况;例如,D3和0 D3以及0 0 D3就是相同的结分方式。
令人惊奇的是一共有42336种不同的结分方式。
当玩家分数小于100时,一共有多少种不同的结分方式?
解题
飞镖盘官网 看到下面的图
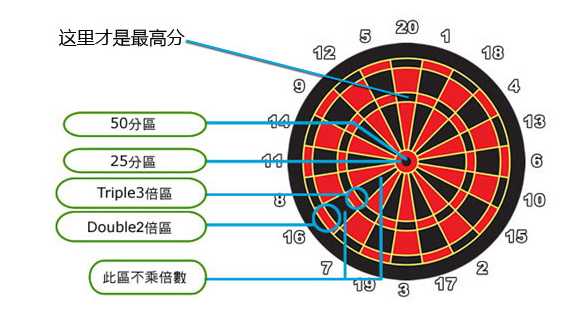
对上面讲的瞬间懂了
理解题意:表盘上的的数组有 1-20、1-20的两倍数、1-20的三倍数、25、50
结分:射击所得分数与自己目前所余分数一样,也就是相减为0,自己是零分。
结分的方式:最后一镖必须射中一个双倍区域
具体分为下面的情况:
1.射击一次结束:一定是双倍数区域
2.射击两次结束:第二次一定是双倍数区域
3.射击三次结束:第三次一定是双倍数区域
Java

package Level4; import java.util.ArrayList; import java.util.List; public class PE0109{ public static void run(){ int limit = 100; int res = 0; List<Integer> scores = new ArrayList<Integer>(); for(int i =1;i<=20;i++){ scores.add(i); scores.add(2*i); scores.add(3*i); } scores.add(25); scores.add(50); List<Integer> doubles = new ArrayList<Integer>(); for(int i=1;i<=20;i++){ doubles.add(2*i); } doubles.add(50); // 射中双倍结束 for(int i=0;i<doubles.size();i++){ if(doubles.get(i) <limit) res++; } // 射击两次结束 for(int i=0;i< scores.size();i++){ for(int j=0;j<doubles.size();j++){ if(scores.get(i)+doubles.get(j) <limit){ res++; } } } // 射击三次结束 for(int i=0;i<scores.size();i++){ for(int j=i;j<scores.size();j++){ for(int k=0;k<doubles.size();k++){ if(scores.get(i)+scores.get(j)+doubles.get(k) <limit){ res++; } } } } System.out.println(res); } public static void main(String[] args){ long t0 = System.currentTimeMillis(); run(); long t1 = System.currentTimeMillis(); long t = t1 - t0; System.out.println("running time="+t/1000+"s"+t%1000+"ms"); } }
38182
running time=0s8ms
Python
# coding=gbk def run1(): from itertools import combinations_with_replacement CHECKOUT_LIMIT = 100 # define dart combinations SINGLE = range(1, 20+1) DOUBLE = [2*i for i in SINGLE] + [50] TREBLE = [3*i for i in SINGLE] ANY_SCORE = SINGLE + [25] + DOUBLE + TREBLE # throw type 1 - 3 darts - hit, hit, double throw1 = [(d1, d2, d3) for (d1, d2) in combinations_with_replacement(ANY_SCORE, 2) for d3 in DOUBLE] # throw type 2 - miss, hit, double throw2 = [(0, d1, d2) for d1 in ANY_SCORE for d2 in DOUBLE] # throw type 3 - miss, miss, double throw3 = [(0, 0, d1) for d1 in DOUBLE] # calculate checkout total that meets conditions checkout_tot = sum(1 for (d1, d2, d3) in throw1 + throw2 + throw3 if sum((d1, d2, d3)) < CHECKOUT_LIMIT) print checkout_tot def run(): res = 0 singles = [] doubles = [] trebles = [] for i in range(1, 21): singles.append(i) doubles.append(2*i) trebles.append(3*i) singles.append(25) doubles.append(50) scores = [] scores += singles scores += doubles scores += trebles for s in doubles: if s<100: res+=1 for s1 in scores: for s2 in doubles: if s1+s2 < 100: res+=1 for i in range(len(scores)): for j in range(i,len(scores)): for s in doubles: if scores[i] + scores[j] + s< 100: res+=1 print res if __name__ == ‘__main__‘: run() run1()
标签:
原文地址:http://www.cnblogs.com/theskulls/p/5153903.html