标签:
一、矩阵
1、定义和简单使用(一般的编程语言,数组下标都是从0开始的,但是MATLAB是从1开始的)
>> a=[1 4 7; 2 5 8; 3 6 9] a = 1 4 7 2 5 8 3 6 9 >> b=[2 3 4;3 4 5;4 5 3]; >> c=[1;2;3]; >> a+b ans = 3 7 11 5 9 13 7 11 12 >> a*b ans = 42 54 45 51 66 57 60 78 69 >> a*c ans = 30 36 42
2、常用矩阵运算和函数
A‘:矩阵转置;
A+B,A-B,A*b:矩阵加减;
inv(A):矩阵求逆;
rank(A):矩阵的秩;
B/A:等价于B*inv(a);
A.*B:点乘,即对应元素相乘;
A(i,:),A(:,j):第i行,第j列;
zeros(n):n阶零矩阵;
eye(n):单位矩阵;
[X,D]=eig(A):X,特征向量,D,特征值
A([i,j],:)=A([j,i],:0):第i行和第j行交换位置;
二、极限(limit),求导(diff),积分(int)
>> F=sym(‘(1+a/x)^x‘); >> limit(F,‘x‘,inf,‘left‘) ans = exp(a) >> syms x; >> y=log((x+2)/(1-x)); >> diff(y,x) ans = ((1/(x - 1) - (x + 2)/(x - 1)^2)*(x - 1))/(x + 2) >> diff(y,x,3) ans = (2*(1/(x - 1) - (x + 2)/(x - 1)^2)*(x - 1))/(x + 2)^3 - (2*(2/(x - 1)^2 - (2*(x + 2))/(x - 1)^3))/(x + 2) - (2*(1/(x - 1) - (x + 2)/(x - 1)^2))/(x + 2)^2 + (2*(2/(x - 1)^2 - (2*(x + 2))/(x - 1)^3)*(x - 1))/(x + 2)^2 + ((6/(x - 1)^3 - (6*(x + 2))/(x - 1)^4)*(x - 1))/(x + 2) >> y=x^5+y^3-sqrt(x)/4; >> int(y) Warning: Explicit integral could not be found. ans = int(log(-(x + 2)/(x - 1))^3, x) - x^(3/2)/6 + x^6/6 >> pretty(ans) 3 - / 2 6 | / x + 2 \3 x x | log| - ----- | dx - -- + -- / \ x - 1 / 6 6
三、绘图
常用的绘图函数有fplot,plot,plot3,mesh,还有一个辅助函数meshgrid。fplot是根据一个已知的函数表达式画图,plot是画一个二维图,已知x,y的坐标,plot3是画三维图,mesh是画有颜色的三维网状(将空间中每三个点连成一个三角片)图。
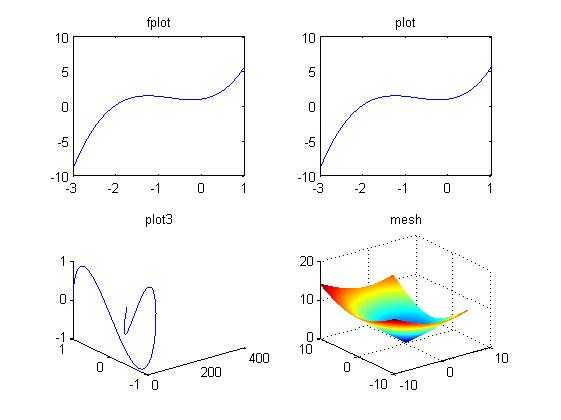
fplot(‘x^3+2*x^2+exp(x)‘,[-3,1]); subplot(2,2,1); fplot(‘x^3+2*x^2+exp(x)‘,[-3,1]); title(‘fplot‘); x=-3:0.1:1; y=x.^3+2*x.^2+exp(x); subplot(2,2,2); plot(x,y); title(‘plot‘); t=0:0.1:6; x=t.^3; y=cos(t); z=sin(2*t); subplot(2,2,3); plot3(x,y,z); title(‘plot3‘); subplot(2,2,4); x=-10:0.1:5; y=-10:0.1:10; [x,y]=meshgrid(x,y); z=sqrt(x.^2+y.^2); mesh(x,y,z); title(‘mesh‘);
运行(F5)结果如图所示:
标签:
原文地址:http://www.cnblogs.com/guanking19/p/5157074.html