标签:
#include <stdio.h> #include <stdlib.h> #include <string.h> #define MAXNODE 100 struct TreeNode { int element,height; struct TreeNode *left; struct TreeNode *right; }; int node[MAXNODE+1]; typedef struct TreeNode Tree; int MAX(int m,int n) { //判断两个数大小的函数 return m>=n?m:n; } int Height(Tree *position) { //返回节点的高度的函数 if(position==NULL) return -1; else return position->height; } Tree *Find(Tree *T,int n) { //查找节点并返回其在树中位置的函数 if(T!=NULL) { if(n==T->element) return T; else if(n<T->element) return Find(T->left,n); else return Find(T->right,n); } return NULL; } Tree *SingleRotateWithLeft(Tree *k2) //名字叫Left是因为累赘在左边 { //实现右单旋转的函数 Tree *k1; k1=k2->left; k2->left=k1->right; k1->right=k2; k2->height=MAX(Height(k2->left),Height(k2->right))+1; k1->height=MAX(Height(k1->left),Height(k2->right))+1; return k1;//返回旋转后的父节点 } Tree *SingleRotateWithRight(Tree *k1) { //实现左单旋转的函数 Tree *k2; k2=k1->right; k1->right=k2->left; k2->left=k1; k1->height=MAX(Height(k1->left),Height(k1->right))+1; k2->height=MAX(Height(k2->left),Height(k2->right))+1; return k2;//返回旋转后的父节点 } Tree *DoubleRotateWithLeft(Tree *k) //名字叫Left是因为累赘在左边 { //实现左右双旋转的函数 k->left=SingleRotateWithRight(k->left); return SingleRotateWithLeft(k); } Tree *DoubleRotateWithRight(Tree *k) { //实现双右左旋转的函数 k->right=SingleRotateWithLeft(k->right); return SingleRotateWithRight(k); } Tree *InsertSearchTree(Tree *T,int n) { //将节点插入二叉查找树的函数 if(T==NULL) { T= malloc(sizeof(Tree)); if(T==NULL) exit(0); T->element=n; T->height=0; T->left=T->right=NULL; } else if(n<T->element) T->left=InsertSearchTree(T->left,n); else if(T->element<n) T->right=InsertSearchTree(T->right,n); T->height=MAX(Height(T->left),Height(T->right))+1; return T; } Tree *InsertAvlTree(Tree *T,int n) { //将节点插入avl树的函数 if(T==NULL) { T= malloc(sizeof(Tree)); if(T==NULL) exit(0); T->element=n; T->height=0; T->left=T->right=NULL; } else if(n<T->element) { T->left=InsertAvlTree(T->left,n); if(Height(T->left)-Height(T->right)>1) { if(n<T->left->element) T=SingleRotateWithLeft(T); else T=DoubleRotateWithLeft(T); } } else if(n>T->element) { T->right=InsertAvlTree(T->right,n); if(Height(T->right)-Height(T->left)>1) { if(n<T->right->element) T=DoubleRotateWithRight(T); else T=SingleRotateWithRight(T); } } T->height=MAX(Height(T->left),Height(T->right))+1; return T; } Tree *Revise(Tree *T) { //将一颗二叉查找树变成avl的函数 if(T==NULL) return NULL; T->left=Revise(T->left); T->right=Revise(T->right); T->height=MAX(Height(T->left),Height(T->right))+1; if(Height(T->left)-Height(T->right)>1) { if(Height(T->left->left)>=Height(T->left->right)) T=SingleRotateWithLeft(T); else T=DoubleRotateWithLeft(T); } else if(Height(T->right)-Height(T->left)>1) { if(Height(T->right->right)>=Height(T->right->left)) T=SingleRotateWithRight(T); else T=DoubleRotateWithRight(T); } return T; } int IsAvlTree(Tree *T) { //判断二叉查找树是不是avl树的函数 if(T!=NULL) { if(Height(T->left)-Height(T->right)>1||Height(T->right)-Height(T->left)>1) return -1; if(IsAvlTree(T->left)==-1||IsAvlTree(T->right)==-1) return -1; } return 0; } void Travel(Tree *T) { //遍历avl树并按照先序遍历输出各节点的函数 if(T!=NULL) printf("%d",T->element); Travel(T->left); Travel(T->right); } Tree *Delete(Tree *T,int n) { //将树中指定节点删除的函数 Tree *tmp; if(T==NULL) return NULL; if(T->element==n) { if(T->right==NULL) { tmp=T; T=T->left; free(tmp); } else { tmp=T->right; while(tmp->left!=NULL) tmp=tmp->left; T->element=tmp->element; T->right=Delete(T->right,tmp->element); //这个函数没弄明 T->height = MAX(Height(T->left),Height(T->right)) + 1; } return T; } if(n < T->element) T->left = Delete(T->left,n); else T->right = Delete(T->right,n); T->height = MAX(Height(T->left),Height(T->right)) + 1; return T; } Tree *MakeEmpty(Tree *T) { //将树中各节点清空的函数 if(T!=NULL) { MakeEmpty(T->left); MakeEmpty(T->right); free(T); } return NULL }
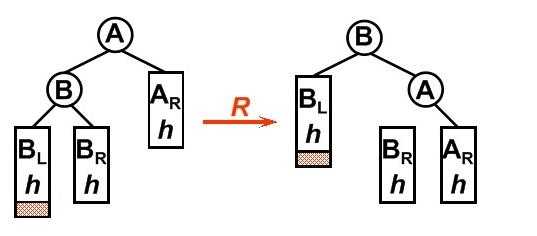
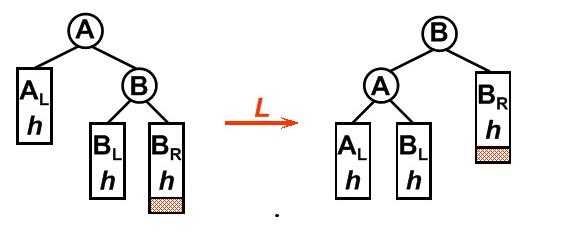
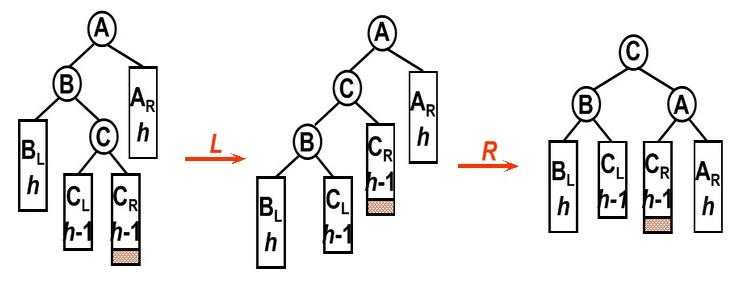
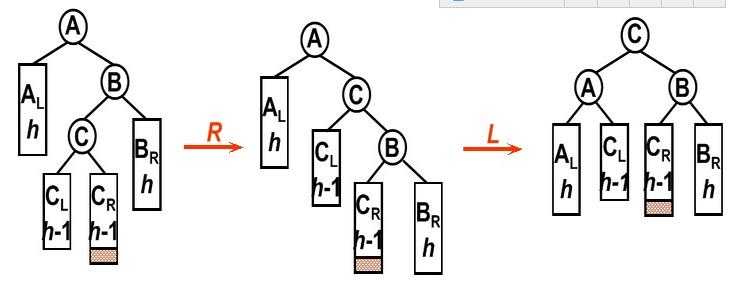
//后面四幅图分别对应代码中四种旋转函数
标签:
原文地址:http://www.cnblogs.com/CClarence/p/5158982.html