标签：
在数论，对正整数n，欧拉函数是小于n的数中与n互质的数的数目。
首先我们给出欧拉函数的通式：
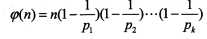其中p1, p2……pk为n的所有质因数，n是不为0的整数。
以上式子是如何得到的呢？
下面给出证明：
先将n分解质因数为
然后利用容斥原理来减去p1、p2……pk的倍数的个数，即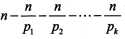
。
然后我们加上同时时两个因数的倍数的数的个数，即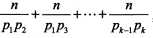
再减去同时为三个因数的数的个数……即可总结出如下公式
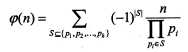
接着便可变形为以上给出的欧拉函数的通式。
标签：
原文地址：http://www.cnblogs.com/wls001/p/5163018.html
