标签:
参考文献:https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E6%A0%91
1,N0=N2+1
N = N0 + N1 + N2; N = E + 1; E = N1*1 + N2*2; -> N0 = N2 + 1;
2,满二叉树和完全二叉树
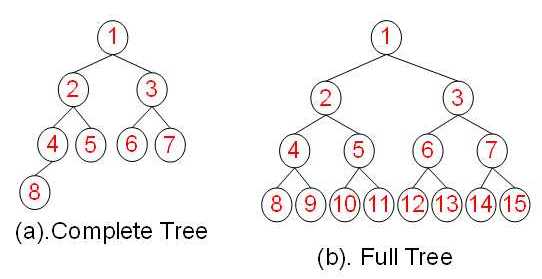
| 满二叉树 | 完全二叉树 | |
| 总节点数 k | 2h-1 <= k < 2h-1 | k = 2h - 1 |
| 树高 h | h = log2k + 1 | h = log2(k + 1) |
3,遍历
用二叉树表示下述表达式:a+b*(c-d)-e/f
4,深度优先遍历
节点进行深度优先搜索的顺序:
利用深度优先搜索算法可以产生目标图的相应拓扑排序表,利用拓扑排序表可以方便的解决很多相关的图论问题,如最大路径问题等等。

5,广度优先搜索
节点进行广度优先搜索的顺序:

6,将n叉树转换为二叉树

注:
7,赫夫曼树
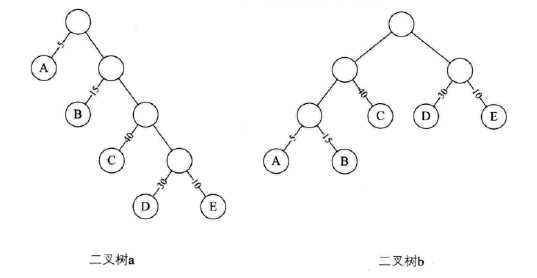
7.1:路径长度:从树中一个结点到另一个结点之间的分支构成两个结点之间的路径,路径上的边的数目;
7.2:树的路径长度:就是从根结点到每一结点的路径长度之和;
例如:
a = 1+1+2+2+3+3+4+4=20
b = 1+2+3+3+2+1+2+2=16
7.3:节点的带权路径长度:结点到树根之间的路径长度与该结点上权的乘积;
7.4:树的带权路径长度:树中所有叶子节点的带权路径长度之和。其中带权路径长度WPL最小的二叉树称作赫夫曼树。
例如:
二叉树a的WPL=5*1+15*2+40*3+30*4+10*4=315
二叉树b的WPL=5*3+15*3+40*2+30*2+10*2=220
7.5:构造赫夫曼树:
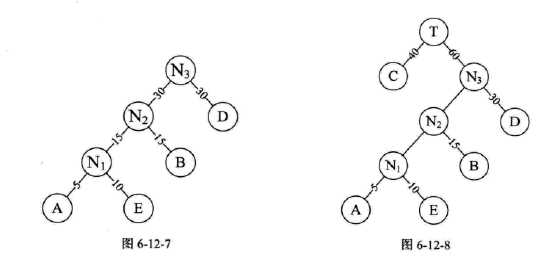
注:每一步考虑的权值为权值之和:例如N1=A+E=15
标签:
原文地址:http://www.cnblogs.com/lemon-now/p/5166573.html