标签:
用少量数据来概括大量数字是日常生活中常见的。那么可以用少量所谓汇总统计量或概括统计量(summary statistic)来描述定量变量的数据。任何样本的函数,只要不包含总体的未知参数,都称为统计量(statistic),那么样本的随机性决定了统计量的随机性。
数据的"位置"
比如说哪个地方穷,那个地方富,哪个国家人高,哪个国家人矮,这样不是说一个地方的所有人都比另一个地方的所有人富有或高,仅仅忽略了"平均起来"这样的字眼。实际上,这种说法是关于数据中某变量观测值的"中心位置",或者数据分布的中心(center或center tendency)的某种表述。这种与"位置"的有关统计量就称为位置统计量(location statistic)。
最常用的位置统计量就是小学学到的平均值,在统计学中叫做"均值",严格地说叫做样本平均值(sample mean)。
数据的"尺度"
是否"均"是由尺度统计量(scale statistic)来描述的。尺度统计量是描述数据散布,即描述集中于分散程度或变化的度量。一般来说,数据越分散,尺度统计量的值越大。
最简单的尺度统计量就是极差(range)。极差就是极大值和极小值之间的差。
另一个常用的尺度统计量为(样本)标准差(standard deviation)。它度量样本中各个数值到均值的距离的一种平均。简单来说,标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。标准差实际上是方差的平方根。样本方差是由各观测值到均值距离的平方和除以减去1的样本量。比如:如果样本中的观测值为X1,X2,X3,X4....Xn,则样本方差为:
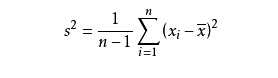
那么标准差就为样本方差的平方根:
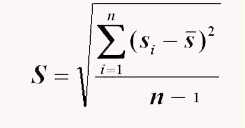
显然如果标准差越大,数据中的观测值就越分散,小的标准值就意味着数据很集中。
数据的标准得分
比如,数据给出两个版的同一们课的成绩,假定两个班水平类似,但是由于两个任课老师的评分标准不同,使得两个班成绩的均值和标准差都不一样。例如,1班的均值和标准差分别为78.53和9.43,而2班的均值和标准差分别为70.19和7.00。那么得到90分的一班的yangsy是不是就比2班的xiaojingjing成绩更好呢?怎样比较菜合理呢?
虽然这种均值和标准差的值不能够直接比较,但是可以把它们标准化,然后再比较标准化的数据。一个标准化的方法是把某样本原始观测值(得分)和该样本均值之差除以该样本的标准差,得到的度量成为标准得分(standard score)即,某观测值Xi的标准得分Zi定义为: z=(x- EX)/σ
转换成相应的标准得分,就可以进行比较了。那么在上述例子中yangsy的得分(90-78.53)/9.43 = 1.22 ,而xiaojingjing的标准得分为(82 - 70.19)/7 = 1.69。所以xiaojingjing的分数应该优于yangsy。
当然,在应用一些统计方法时,有时的确需要对数据做标准化或其他变换,但这些都不是随意的,都有某些确定的理论基础和实践目的。
众数、中位数、平均值的联系与区别:
1、平均值是通过计算得到的,因此它会因每一个数据的变化而变化。
2、中位数是通过排序得到的,它不受最大、最小两个极端数值的影响.中位数在一定程度上综合了平均数和中位数的优点,具有比较好的代表性。部分数据的变动对中位数没有影响,当一组数据中的个别数据变动较大时,常用它来描述这组数据的集中趋势。另外,因中位数在一组数据的数值排序中处中间的位置,
3、众数也是数据的一种代表数,反映了一组数据的集中程度.日常生活中诸如“最佳”、“最受欢迎”、“最满意”等,都与众数有关系,它反映了一种最普遍的倾向.
平均数、中位数和众数它们都有各自的的优缺点.
平均数:(1)需要全组所有数据来计算;
(2)易受数据中极端数值的影响.
中位数:(1)仅需把数据按顺序排列后即可确定;
(2)不易受数据中极端数值的影响.
众数:(1)通过计数得到;
(2)不易受数据中极端数值的影响
标签:
原文地址:http://www.cnblogs.com/yangsy0915/p/5168256.html