标签:
我们知道,混合线性模型是一般线性模型的扩展,而广义线性模型在混合线性模型的基础上又做了进一步扩展,使得线性模型的使用范围更加广阔。每一次的扩展,实际上都是模型适用范围的扩展,一般线性模型要求观测值之间相互独立、残差(因变量)服从正态分布、残差(因变量)方差齐性,而混合线性模型取消了观测值之间相互独立和残差(因变量)方差齐性的要求,接下来广义线性模型又取消了对残差(因变量)服从正态分布的要求。残差不一定要服从正态分布,可以服从二项、泊松、负二项、正态、伽马、逆高斯等分布,这些分布被统称为指数分布族,并且引入了连接函数,根据不同的因变量分布、连接函数等组合,可以得到各种不同的广义线性模型。
要注意,虽然广义线性模型不要求因变量服从正态分布,但是还是要求相互独立的,如果不符合相互独立,需要使用后面介绍的广义估计方程。
=================================================
一、广义线性模型
广义线性模型的一般形式为: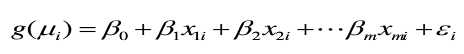
有以下几个部分组成
1.线性部分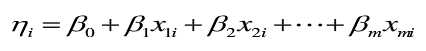
2.随机部分εi
3.连接函数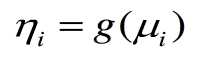
连接函数为单调可微(连续且充分光滑)的函数,连接函数起了"y的估计值μ"与"自变量的线性预测η"的作用,在一般线性模型中,二者是一回事,但是当自变量取值范围受限时,就需要通过连接函数扩大取值范围,因此在广义线性模型中,自变量的线性预测值是因变量的函数估计值。
广义线性模型设定因变量服从指数族概率分布,这样因变量就可以不局限于正态分布一种形式,并且方差可以不稳定。
指数分布族的概率密度函数为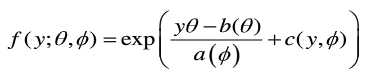
其中θ和φ为两个参数,θ为自然参数,φ为离散参数,a,b,c为函数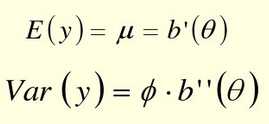
广义线性模型的参数估计:
广义线性模型的参数估计一般不能使用最小二乘法,常用加权最小二乘法或极大似然法。回归参数需要用迭代法求解。
广义线性模型的检验和拟合优度:
广义线性模型的检验一般使用似然比检验、Wald检验。模型的比较用似然比检验,回归系数使用Wald检验。
似然比检验是通过比较两个相嵌套模型(如模型P嵌套在模型K内)的对数似然函数来进行的,其统计量为G:
G=-2*(lp-lk)
lp是模型P的对数似然函数,lk是模型k1的对数似然函数
模型P中的自变量是模型K中自变量的一部分,另一部分就是要检验的变量,这里G服从自由度为K-P的卡方分布。
广义线性模型的拟合优度通常使用以下统计量来度量:
离差统计量,pearson卡方统计量,AIC,AICC,BIC,CAIC准则,准则的值越小越好
标签:
原文地址:http://www.cnblogs.com/xmdata-analysis/p/5173511.html