平衡查找树（2-3-4 树）

标签：style   blog   http   os   strong   width   2014   re   

二叉查找树（Binary Search Tree）在很多情况下可以良好的工作，但它的限制是最坏情况下的渐进运行时间为 O(n)。

平衡查找树（Balanced Search Tree）的设计则是保证其高度在最坏的情况下为 O(log n)，其插入、删除和查找可以实现渐进运行时间 O(log n)。

现在其实存在很多种类的平衡查找树，常见的有 AVL树、红黑树、B 树等。

不同的平衡查找树的高度（height）：

• AVL 树：高度 ≤ (1.44042..)log₂ n
• 红黑树：高度 ≤ 2*log₂ (n+1)
• 2-3 树：高度 ≤ log₂ n
• 2-3-4 树：高度 ≤ log₂ n

2-3 树

2-3 树中节点和存储的元素符合如下特性要求：

1. 任一节点只能是 2 度节点或 3 度节点，不存在元素数为 0 的节点。
   • 2 度节点：包含 1 个元素的节点将只能有 2 个子节点；
   • 3 度节点：包含 2 个元素的节点将只能有 3 个子节点；
2. 所有叶子节点都拥有相同的深度（depth）。
3. 元素始终保持排序顺序。

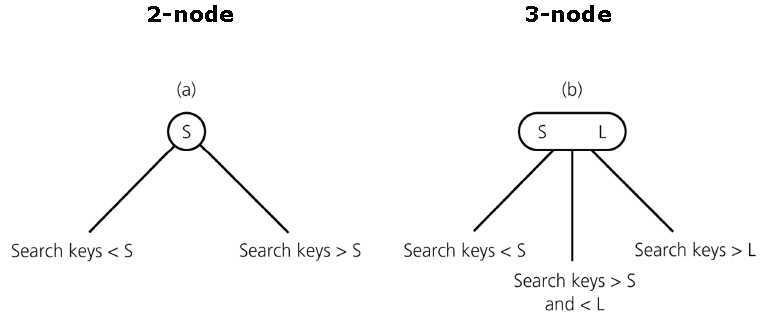
相比二叉查找树，2-3 树的优势：

2-3 树可以获得更好的渐进查找时间 O(log₂ n)。

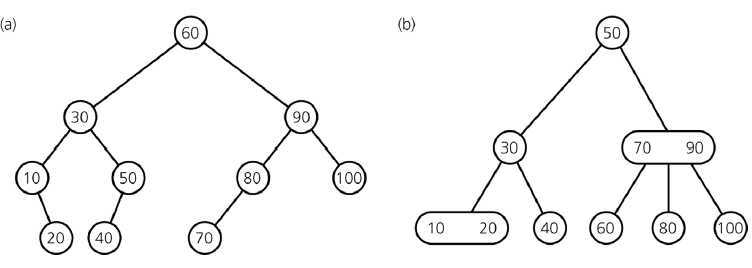
2-3 树更容易保持树的平衡。

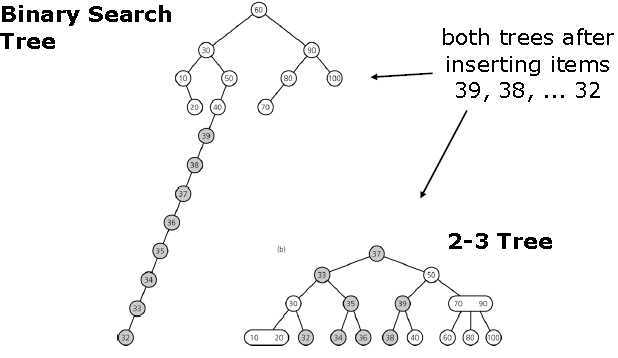
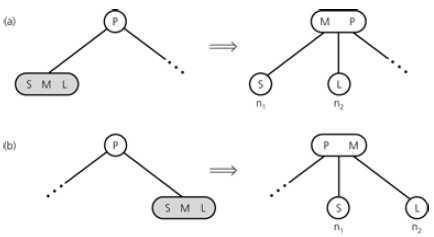
插入操作

将元素 I 插入到 2-3 树中，需要如下步骤：

1. 定位元素 I 应被插入的叶子节点的位置；
2. 将 I 插入到该叶子节点中；
3. 如果叶子节点此时仅包含 2 个元素，则插入操作结束；
4. 如果叶子节点此时包含 3 个元素，则需要分裂叶子节点成两个新的节点；

2-3-4 树（2-4 树）

2-3-4 树中节点和存储的元素符合如下特性要求：

1. 任一节点只能是 2 度节点、3 度节点或 4 度节点，不存在元素数为 0 的节点。
   • 2 度节点：包含 1 个元素的节点将只能有 2 个子节点；
   • 3 度节点：包含 2 个元素的节点将只能有 3 个子节点；
   • 4 度节点：包含 3 个元素的节点将只能有 4 个子节点；
2. 所有叶子节点都拥有相同的深度（depth）。
3. 元素始终保持排序顺序。

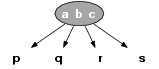
          2 度节点                          3 度节点                            4 度节点

其中，每个子节点仍是一棵 2-3-4 树，但子节点可能为空。

在 2-3-4 树中，所有叶子节点都在同一层，也就是最底层。但是元素却可以出现在所有节点中，也就是说，即使是叶子节点，也可以包含1、2 或 3 个元素，但不能没有元素。2-3-4 树保持着完美的平衡，每一条到叶子节点的路径都是等长的。

非叶子节点必须拥有至少 1 个子节点。设节点的子节点的数量为 L，节点包含元素的数量为 D，则：L = D + 1 。

因为 2-3-4 树中的节点至多包含 4 个子节点，所以该树叶称为 4 阶多路树（multiway tree of order 4）。

查找节点

在 2-3-4 树中查找结点，分为以下几个步骤：

1. 将被查找的元素与节点中存储的元素进行比较；
2. 查找包含被查找元素的区间；
3. 若区间存在，则移至子节点，回到第 1 步继续查找；

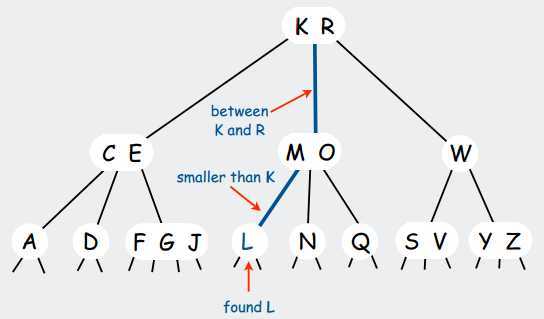插入节点

插入节点时，将从根节点开始查找，步骤如下：

1. 如果当前节点为 4 度节点（也就是有 3 个元素）：
   • 移除并保存节点中间的元素值，然后生成一个 3 度节点（仅有 2 个元素）；
   • 将该 3 度节点分裂成一对 2 度节点（仅有 1 个元素）；
   • 如果当前节点是根节点：
     • 被保存的中间值将被设置为新的根节点，该根节点为 2 度节点，则树的高度将增加 1；
   • 否则，将中间值加入父节点中。
2. 查找子节点中可以包含被插入值的区间；
3. 如果找到的节点是一个叶子节点，则将被插入值放入该节点中，插入操作结束；
   • 否则，继续查找子节点，或回到步骤 1。

例如，现在要将值 "25" 插入到如下的 2-3-4 树中：

从根节点（10,20）开始查找，向子树查找，直到找到子节点（22,24,29）。因为区间（20,∞）包含 25。

节点（22,24,29）是一个 4 度节点，所以将其中间值 24 推到父节点中。

剩下的 3 度节点（22,29）将被分裂成一对 2 度节点，也就是（22）和（29）。新的父节点为（10,20,24）。

在下降到右侧子节点（29）。因为区间（24-29）包含 25。

节点（29）没有左孩子。可将 25 直接插入到该节点中，插入完毕。

节点的分裂方式

将 4 度节点分裂的方式如下：

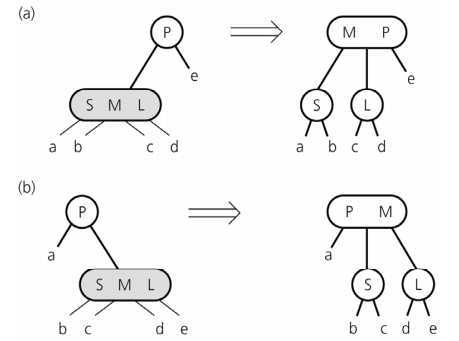
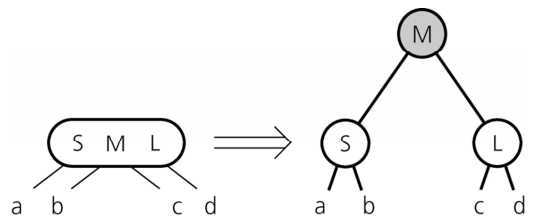如果一个 4 度节点的父节点是一个 2 度节点，则将按如下方式分裂 4 度节点：

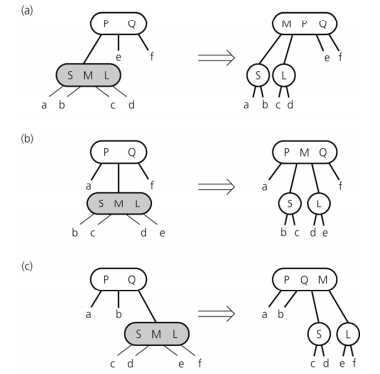
如果一个 4 度节点的父节点是一个 3 度节点，则将按如下方式分裂 4 度节点：

删除节点

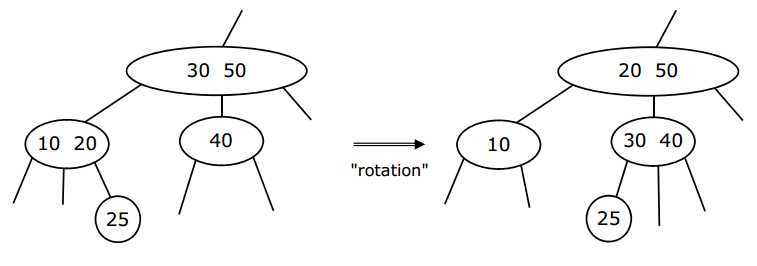
情况1：临近兄弟节点是 3 度节点或 4 度节点。

解决方案：通过旋转操作和移动子树来从临近节点偷元素（steal）。

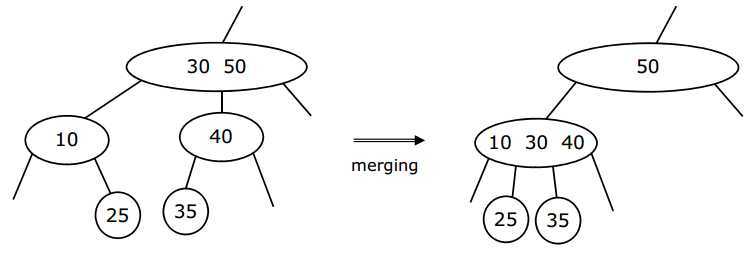
情况2：临近兄弟节点是 2 度节点。

解决方案：通过与临近兄弟节点合并，并从父节点偷元素。

参考资料

• Binary logarithm
• 2–3 tree
• 2–3–4 tree
• AA tree
• Balanced Trees

本文《平衡查找树》由 Dennis Gao 发表自博客园博客，任何未经作者本人允许的人为或爬虫转载均为耍流氓。

平衡查找树（2-3-4 树）,布布扣,bubuko.com

平衡查找树（2-3-4 树）

标签：style   blog   http   os   strong   width   2014   re   

原文地址：http://www.cnblogs.com/gaochundong/p/balanced_search_tree.html