标签:
图有两种表示方法,邻接矩阵和邻接表,接下来我们讲解邻接矩阵和用c实现一个邻接矩阵.
我们先看一个图:
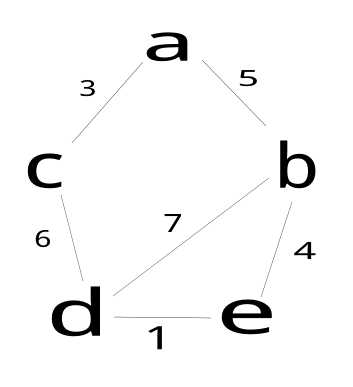
我们想将这样一个图信息存储起来,我们有两个必须存储的数据,节点信息(a,b,c,d,e)和权值(3,5,4,1,6,7)和节点之间的关系.权值也就是路径.
邻接矩阵表示法,用两个数组表示,一个一维数组和一个二维数组.
一维数组存储节点信息,二维数组存储节点之间的关系.
将上图转换成一个邻接矩阵

接下来我们看一看邻接矩阵是的结构体.
typedef struct matrix { node_type vertex[MAX_NUM];//节点信息 int arcs[MAX_NUM][MAX_NUM];//矩阵 int vertexs, brim;//节点数,边数 } Graph;
我们将node_type设为char类型,方便明了.但在输入字符后,我们通常回输出空格或者回车符,在向字符变量输入字符时,我们要将之前输入的空格或者回车符从缓冲区中清楚,这也就是程序中getchar()的用处.
我们先构造一个邻接矩阵
1)输入节点数和节点信息,构造上图的两个数组.(将二维数组初始化MAX)
2)输入某个节点的相邻节点和权值(通过下标找到在二维数组中相应的位置,将权值输入)
void g_create(Graph * graph) { int num; int i, j, k; char c; printf("输入节点个数:"); scanf("%d", &graph->vertexs); getchar();//接受回车键 printf("输入节点信息:"); for ( i = 0; i < graph->vertexs; i++ ) { scanf("%c", &graph->vertex[i]); getchar(); } for ( i = 0; i < graph->vertexs; i++ )//初始化矩阵 for ( j = 0; j < graph->vertexs; j++ ) graph->arcs[i][j] = MAX_VALUE; graph->brim = 0;//初始化边数 // i 代表行数, j 是用来循环的, k 代表列数 for ( i = 0; i < graph->vertexs; i++ ) { printf("输入与%c节点相邻的节点与权值,输入#号键结束\n", graph->vertex[i]); for ( j = 0; j < graph->vertexs; j++ ) { scanf("%c", &c); if ( c == ‘#‘ ) { getchar(); break; } scanf("%d", &num); for ( k = 0; k < graph->vertexs; k++ ) { if ( graph->vertex[k] != c ) continue; graph->arcs[i][k] = num; graph->brim++; } getchar(); } } graph->brim /= 2; }
"// i 代表行数, j 是用来循环的, k 代表列数"下面的代码是将输入的边和权值的信息存储在二维数组中.
i 代表的是在一维数组中的节点的位置,也是二维数组中行.(例如:与a相邻的节点有两个,b和c.这时i=0,代表以为数组中第一个位置,j用来循环输入边和权值,因为我们不知道每个节点都有多少个相邻节点.当输入‘#‘号时结束输入.k是为了将输入的相邻节点与一维数组中的节点信息匹配,如果存在这个节点,这时将权值输入到二维数组中,而 i 是二维数组的行, k 是二维数组的列.然后我们将边数+1,因为a 的相邻节点是 b ,而 b 的相邻节点是 a, 这时我们对边增加了两次,所以在构造邻接矩阵最后将边数除以2.)
深度优先遍历
深度优先遍历是通过递归来实现,与二叉树的遍历有点像.
1)以某一节点开始,访问该节点
2)以该节点开始,重复1.(这里需要定义一个节点数大小的bool类型数组,来记录哪些节点访问过了,哪些节点没有访问过.)
3)当某个节点的邻接节点都访问过了,回退到上一个节点,访问上一个节点的其他相邻节点.
4)重复3.直至返回开始节点.
这是连通图的遍历方法,对于非连通图,我们只需循环调用递归,直至所有节点都访问过.
实现算法:
1)先创建一个visited数组,初始化为false.
2)调用遍历函数,实现递归.
3)当相邻节点为false时,以该节点进行递归.
4)否则返回上一节点
1 //深度优先遍历 2 static void dfs_graph(Graph * graph, bool visited[], const int i); 3 void g_depth_first_search(Graph * graph) 4 { 5 bool visited[graph->vertexs]; 6 int i; 7 for ( i = 0; i < graph->vertexs; i++ ) 8 visited[i] = false; 9 visited[0] = true; 10 dfs_graph(graph, visited, 0); 11 printf("\n"); 12 } 13 14 static void dfs_graph(Graph * graph, bool visited[], const int i) 15 { 16 int j; 17 printf("%c\t", graph->vertex[i]); 18 for ( j = 0; j < graph->vertexs; j++ )//依次检查矩阵 19 { 20 if ( graph->arcs[i][j] != MAX_VALUE && !visited[j] )//i 代表矩阵的行, j 代表矩阵的列 21 { 22 visited[j] = true; 23 dfs_graph(graph, visited, j); 24 } 25 } 26 }
图例:

广度优先遍历
广度优先遍历通过队列实现.
1)从摸一节点开始,将该节点入队,找到该节点的所有相邻节点,将他们入队.
2)将该节点出队,再将队头节点的所有相邻节点入队.(这里也需要一个visited数组,已经入队过的节点不再入队.)
3)检查队列,对队头元素进行操作,出队.
1 void g_breadth_first_search(Graph * graph) 2 { 3 Queue queue;//队列存储的是节点数组的下标(int) 4 bool visited[graph->vertexs]; 5 int i, pos; 6 7 q_init(&queue); 8 for ( i = 0; i < graph->vertexs; i++ ) 9 visited[i] = false; 10 11 visited[0] = true; 12 q_push(&queue, 0); 13 while ( !q_empty(&queue) ) 14 { 15 pos = q_front(&queue); 16 printf("%c\t", graph->vertex[pos]); 17 for ( i = 0; i < graph->vertexs; i++ )//把队头元素的邻接点入队 18 { 19 if ( !visited[i] && graph->arcs[pos][i] != MAX_VALUE ) 20 { 21 visited[i] = true; 22 q_push(&queue, i); 23 } 24 } 25 q_pop(&queue); 26 } 27 printf("\n"); 28 }
如果队列有问题的同学,可以参考我之前写的队列,我把队列文件直接拷贝过来了.
源码
graph.c
#include <stdio.h> #include <stdlib.h> #include <stdbool.h> #include <limits.h> #include "aqueue.h" #define MAX_VALUE INT_MAX #define MAX_NUM 100 typedef char node_type; typedef struct matrix { node_type vertex[MAX_NUM];//节点信息 int arcs[MAX_NUM][MAX_NUM];//矩阵 int vertexs, brim;//节点数,边数 } Graph; void g_create(Graph * graph) { int num; int i, j, k; char c; printf("输入节点个数:"); scanf("%d", &graph->vertexs); getchar();//接受回车键 printf("输入节点信息:"); for ( i = 0; i < graph->vertexs; i++ ) { scanf("%c", &graph->vertex[i]); getchar(); } for ( i = 0; i < graph->vertexs; i++ )//初始化矩阵 for ( j = 0; j < graph->vertexs; j++ ) graph->arcs[i][j] = MAX_VALUE; graph->brim = 0;//初始化边数 // i 代表行数, j 是用来循环的, k 代表列数 for ( i = 0; i < graph->vertexs; i++ ) { printf("输入与%c节点相邻的节点与权值,输入#号键结束\n", graph->vertex[i]); for ( j = 0; j < graph->vertexs; j++ ) { scanf("%c", &c); if ( c == ‘#‘ ) { getchar(); break; } scanf("%d", &num); for ( k = 0; k < graph->vertexs; k++ ) { if ( graph->vertex[k] != c ) continue; graph->arcs[i][k] = num; graph->brim++; } getchar(); } } graph->brim /= 2; } void g_printMatrix(Graph * graph)//打印矩阵状态 { int i, j; for ( i = 0; i < graph->vertexs; i++ ) { for ( j = 0; j < graph->vertexs; j++ ) { printf("%-10d ", graph->arcs[i][j]); } printf("\n"); } } //深度优先遍历 static void dfs_graph(Graph * graph, bool visited[], const int i); void g_depth_first_search(Graph * graph) { bool visited[graph->vertexs]; int i; for ( i = 0; i < graph->vertexs; i++ ) visited[i] = false; visited[0] = true; dfs_graph(graph, visited, 0); printf("\n"); } static void dfs_graph(Graph * graph, bool visited[], const int i) { int j; printf("%c\t", graph->vertex[i]); for ( j = 0; j < graph->vertexs; j++ )//依次检查矩阵 { if ( graph->arcs[i][j] != MAX_VALUE && !visited[j] )//i 代表矩阵的行, j 代表矩阵的列 { visited[j] = true; dfs_graph(graph, visited, j); } } } //广度优先遍历 void g_breadth_first_search(Graph * graph) { Queue queue;//队列存储的是节点数组的下标(int) bool visited[graph->vertexs]; int i, pos; q_init(&queue); for ( i = 0; i < graph->vertexs; i++ ) visited[i] = false; visited[0] = true; q_push(&queue, 0); while ( !q_empty(&queue) ) { pos = q_front(&queue); printf("%c\t", graph->vertex[pos]); for ( i = 0; i < graph->vertexs; i++ )//把队头元素的邻接点入队 { if ( !visited[i] && graph->arcs[pos][i] != MAX_VALUE ) { visited[i] = true; q_push(&queue, i); } } q_pop(&queue); } printf("\n"); } int main(void) { Graph graph; g_create(&graph); g_printMatrix(&graph); g_depth_first_search(&graph); g_breadth_first_search(&graph); return 0; }
标签:
原文地址:http://www.cnblogs.com/ITgaozy/p/5187483.html