标签:
3.1 电阻元件、电感元件与电容元件
3.2 储能元件和换路定则
3.3 RC电路的响应
3.4 一阶线性电路暂态分析 的三要素法
3.5 微分电路与积分电路
3.6 RL电路的响应
3.1.2 电感元件
线圈的匝数N愈多,其电感愈大;线圈中单位电流产生的磁通愈大,电感也愈大。
电感:单位电流产生的磁链。
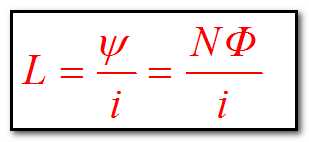

感应电动势eL:具有阻碍电流变化的性质。
电感元件是储能元件,不是耗能元件
电流 i 与磁通Φ、感应电动势 eL与磁通Φ的参考方向之间均符合右螺旋定则。
当电流变化率为零,即线圈通过恒定电流时,电感端电压为零,故电感元件对直流电路视作短路。
电感元件能量: 
在直流电路中,电感的电流不为零。
直流电路中电感相当于短路。
当电压变化率为零时,即电压为恒定电压时,流过电容电流为零,故电容对直流电路视作开路。


电容元件是储能元件(存储电场能),不是耗能元件
电容分为无极性 和 有极性。
直流电路中电容相当于断路
直流电路中电容电压不为零

3.2 储能元件和换路定则
3.2.1 电路中产生暂态过程的条件与原因
暂态过程:电路从一种稳态变化到另一种稳态的 过渡过程。
研究暂态过程的目的:认识和掌握这种客观存在的物理现象的规律,既 要充分利用暂态过程的特性,同时也必须预防它所产生的危害。
电路暂态分析的内容:
1.讨论暂态过程中电压与电流随时间变化的规律。
2.影响暂态过程快慢的电路时间常数。
原稳态 ---> 新稳态 的过渡过程,就是暂态过程。
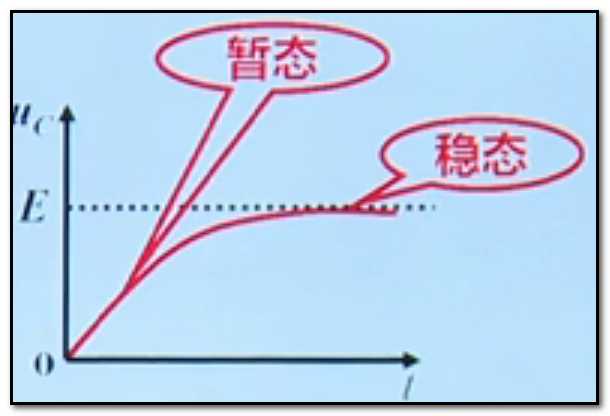
换路:电路的接通、断开、短路、电压改变或参数改变等,使电路中的能量发生变化。
换路瞬间由于储能元件的能量不能跃变而产生。
电感(存储磁场能)元件中储有的磁能 不能跃变,因此电流 iL不能跃变。
电容(存储电场能)元件中储有的电能 不能跃变,因此电压 uC不能跃变。
3.2.2 换路定则
换路定则:电路换路瞬间,电感元件中的电流和电容元件上的电压不能跃变。
能量的存储和释放是需要一个过程的。 储能元件的能量不能突变。
换路定则仅适用于换路瞬间,用来确定t = 0+时电路中电容电压和电感电流之值,即暂态过程的初始值。
初始值分为独立初始条件和非独立初始条件。
求解微分方程是有一些边界条件的。
⒈ 独立初始条件uC(0+)与iL(0+)的确定
⑴画出t = 换路前 (0-的等效电路,稳定状态下:
⑵根据换路定则:

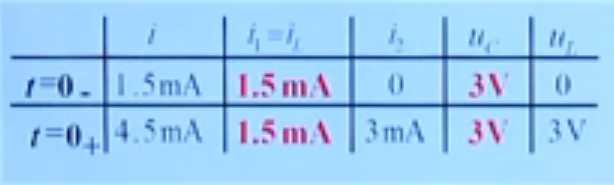
在 换路前后, 电感电流和电容电压 没有变化,其他的是把电感等效成电流源,电容等效成电压源 计算出来的。

3.3 RC电路的响应
经典法:根据激励(电源电压或电流),通过求解电路的微分方程得出电路的响应(电压和电流)。
3.3.1 RC电路的零输入响应
零输入响应:无电源激励,输入信号为零,仅由电容元件的初始状态 uC(0+) 所产生的电路的响应。
实质:分析RC电路的放电过程。

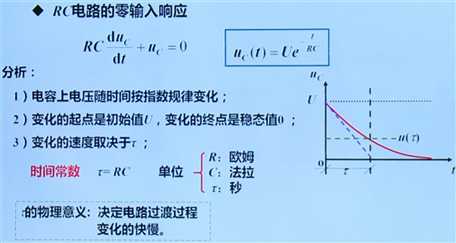
(4)电路中其他物理量也随时间按指数规律变化,且为同一个时间常数。
电路中暂态过程同时发生、同时消失,且电路中各响应具有相同的时间常数。
经过 t =5T的时间,就足可认为电路达到稳态。
工程上认为 t = 3- 5 t 电路就可认为达到稳态。
3.3.2 RC电路的零状态响应
零状态响应:换路前电容无初始储能,换路后仅由电源激励所产生的电路的响应。
实质:分析RC电路的充电过程。
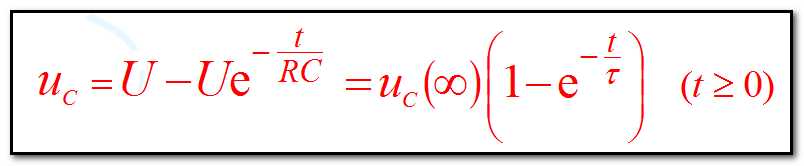
标签:
原文地址:http://www.cnblogs.com/zrui513/p/5188301.html