标签:
原题链接:填数字
顺便推荐一下,偶然看到这个OJ,发现社区运营做得很赞,而且交互和编译环境都很赞(可以编译包括Python,Ruby,Js在内的脚本语言,也可以编译新标准的C/C++11,甚至包括Go和C Sharp等),虽然暂时不太火,但估计会逐渐成为国内算法界非常受欢迎的OJ社区。
主页:http://www.51nod.com/index.html
本题是个题意简单的,思路复杂的DP题,说实话,光是想出这种DP就已经非常不易了,即便写出来也要考虑清楚每一种转移的公式和数值关系。
原题:有n(1-200)行格子,第i(1<=i<=n)行有i个格子,每行格子是左对齐。现在要在每一个格子填入一个非负整数,最后使得每一行每一列的和都不超过2。
请计算有多少种方案,答案比较大,请输出对100,000,007(1e8+7)取余后的结果。
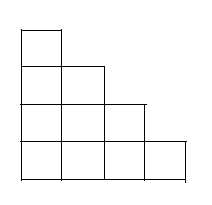
下图是n=4的时候格子的摆放。
1 //务必注意理清每次状态转移方程的思路和公式 2 //本人因为一个地方写多了个+1,结果WA了5发.... 3 //Memory:34900K Time:93Ms 4 #include<iostream> 5 using namespace std; 6 7 #define MAX 201 8 #define MOD 100000007 9 10 #define COL_0 (i - j - k - 1) //和为0的列数 11 /* 12 * dp[i][j][k] 13 * i:表明当前行 14 * j:表明i行完成时有多少列为1 15 * k:表明j行完成时有多少列为2 16 * dp值表明该状态下的情况数 17 * 每次由 i-1行 -> i行 转移同j同k的状态 18 */ 19 __int64 dp[MAX][MAX][MAX]; 20 21 int main() 22 { 23 int n; 24 scanf("%d", &n); 25 dp[1][0][0] = dp[1][1][0] = dp[1][0][1] = 1; 26 for (__int64 i = 2; i <= n; i++) 27 for (__int64 j = 0; j <= i; j++) 28 for (__int64 k = 0; k <= i - j; k++) 29 { 30 //最后一格为0时 31 //-可+2 32 if (i - j - k - 1 >= 1) 33 dp[i][j][k + 1] = (dp[i][j][k + 1] + dp[i - 1][j][k] * COL_0) % MOD; 34 //-可+1 35 //--两个1_0-0 36 if (i - j - k - 1 >= 2) 37 dp[i][j + 2][k] = (dp[i][j + 2][k] + dp[i - 1][j][k] * (COL_0 * (COL_0 - 1) / 2)) % MOD; 38 //--两个1_1-0 39 if (j >= 1 && i - j - k - 1 >= 1) 40 dp[i][j][k + 1] = (dp[i][j][k + 1] + dp[i - 1][j][k] * COL_0 *j) % MOD; 41 //--两个1_1-1 42 if (j >= 2) 43 dp[i][j - 2][k + 2] = (dp[i][j - 2][k + 2] + dp[i - 1][j][k] * (j*(j - 1) / 2)) % MOD; 44 //--一个1_1 45 if (j >= 1) 46 dp[i][j - 1][k + 1] = (dp[i][j - 1][k + 1] + dp[i - 1][j][k] * j) % MOD; 47 //--一个1_0 48 if (i - j - k - 1 >= 1) 49 dp[i][j + 1][k] = (dp[i][j + 1][k] + dp[i - 1][j][k] * COL_0) % MOD; 50 //什么都不加 51 dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j][k]) % MOD; 52 53 //最后一格为1时 54 //-可+1_0 55 if (i - j - k - 1 >= 1) 56 dp[i][j + 2][k] = (dp[i][j + 2][k] + dp[i - 1][j][k] * COL_0) % MOD; 57 //-可+1_1 58 if (j >= 1) 59 dp[i][j][k + 1] = (dp[i][j][k + 1] + dp[i - 1][j][k] * j) % MOD; 60 //什么都不加 61 dp[i][j + 1][k] = (dp[i][j + 1][k] + dp[i - 1][j][k]) % MOD; 62 63 //最后一格为2时 64 dp[i][j][k + 1] = (dp[i][j][k + 1] + dp[i - 1][j][k]) % MOD; 65 } 66 67 __int64 sum = 0; 68 for (int j = 0; j <= n; j++) 69 for (int k = 0; k <= n - j; k++) 70 sum = (sum + dp[n][j][k]) % MOD; 71 printf("%I64d\n", sum); 72 73 return 0; 74 }
ACM/ICPC 之 DP进阶(51Nod-1371(填数字))
标签:
原文地址:http://www.cnblogs.com/Inkblots/p/5189071.html