标签:poj1037
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 6489 | Accepted: 2363 |
Description
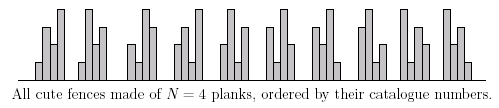
Input
Output
Sample Input
2 2 1 3 3
Sample Output
1 2 2 3 1
#include <stdio.h>
#include <string.h>
#define maxn 22
#define UP 0
#define DOWN 1
int vis[maxn], ans[maxn];
__int64 dp[maxn][maxn][2];
void Init(int n)
{
int i, j, k;
dp[1][1][UP] = dp[1][1][DOWN] = 1;
for(i = 2; i <= n; ++i){ //i is the amount of total sticks
for(j = 1; j <= i; ++j){ //j is the first stick's position
for(k = j; k < i; ++k) //k is the subSolution of dp array
dp[i][j][UP] += dp[i-1][k][DOWN];
for(k = 1; k < j; ++k)
dp[i][j][DOWN] += dp[i-1][k][UP];
}
}
}
void Print(int n, __int64 c)
{
memset(vis, 0, sizeof(vis));
int i, j, k, rank;
__int64 skip = 0, pre = 0;
for(i = 1; i <= n; ++i){ //i is the position to select now
rank = 0; //the rank's min stick
for(j = 1; j <= n; ++j){ //j is the stick to be select
pre = skip;
if(!vis[j]){
++rank;
if(i == 1) skip += dp[n][rank][UP] + dp[n][rank][DOWN];
else if(j > ans[i-1] && (i == 2 || ans[i-2] > ans[i-1]))
skip += dp[n-i+1][rank][DOWN];
else if(j < ans[i-1] && (i == 2 || ans[i-2] < ans[i-1]))
skip += dp[n-i+1][rank][UP];
if(skip >= c) break;
}
}
ans[i] = j;
vis[j] = 1;
skip = pre;
}
for(i = 1; i <= n; ++i)
if(i != n) printf("%d ", ans[i]);
else printf("%d\n", ans[i]);
}
int main()
{
int t, n;
__int64 c;
Init(20);
scanf("%d", &t);
while(t--){
scanf("%d%I64d", &n, &c);
Print(n, c);
}
return 0;
}
#include <stdio.h>
#include <string.h>
#define UP 0
#define DOWN 1
#define maxn 25
long long C[maxn][maxn][2];
//C[i][k][DOWN] 是S(i)中以第k短的木棒打头的DOWN方案数,C[i][k][UP]
//是S(i)中以第k短的木棒打头的UP方案数,第k短指i根中第k短
void Init(int n)
{
memset(C, 0, sizeof(C));
C[1][1][UP] = C[1][1][DOWN] = 1;
int i, k, M, N;
for(i = 2; i <= n; ++i){
for(k = 1; k <= i; ++k){ //枚举第一根木棒的长度
//枚举第二根长度
for(M = k; M < i; ++M) C[i][k][UP] += C[i-1][M][DOWN];
//枚举第二根长度
for(N = 1; N < k; ++N) C[i][k][DOWN] += C[i-1][N][UP];
}
}
//总方案数是 Sum{ C[n][k][DOWN] + C[n][k][UP] } k = 1.. n;
}
void Print(int n, long long cc)
{
long long skipped = 0, oldVal; //已经跳过的方案数
int seq[maxn]; //最终要输出的答案
int used[maxn]; //木棒是否用过
memset(used, 0, sizeof(used));
for(int i = 1, k; i <= n; ++i){ //依次确定位置i的木棒序号
int No = 0;
for(k = 1; k <= n; ++k){ //枚举位置i的木棒
oldVal = skipped;
if(!used[k]){
++No; //k是剩下木棒里的第No短的
if(i == 1) skipped += C[n][No][UP] + C[n][No][DOWN];
//以下寻找合法位置
else if(k > seq[i-1] && (i == 2 || seq[i-2] > seq[i-1]))
skipped += C[n-i+1][No][DOWN];
else if(k < seq[i-1] && (i == 2 || seq[i-2] < seq[i-1]))
skipped += C[n-i+1][No][UP];
if(skipped >= cc) break;
}
}
used[k] = 1;
seq[i] = k;
skipped = oldVal;
}
for(int i = 1; i <= n; ++i)
if(i < n) printf("%d ", seq[i]);
else printf("%d\n", seq[i]);
}
int main()
{
int T, n; long long c;
Init(20);
scanf("%d", &T);
while(T--){
scanf("%d%lld", &n, &c);
Print(n, c);
}
return 0;
}
POJ1037 A decorative fence 【动态规划】,布布扣,bubuko.com
POJ1037 A decorative fence 【动态规划】
标签:poj1037
原文地址:http://blog.csdn.net/chang_mu/article/details/38090743