标签:
在之前初步介绍图的文章中,我们得知,图(graph)是表征事物之间关系的一种抽象化表示方法,而基于图的概念,我们将所有的无回路无向图拿出来,给它们一个新的名字——树。
关于树的概念性术语很多,这里我们先就简单的二叉树(一个根至多有两个子树)来进行分析。
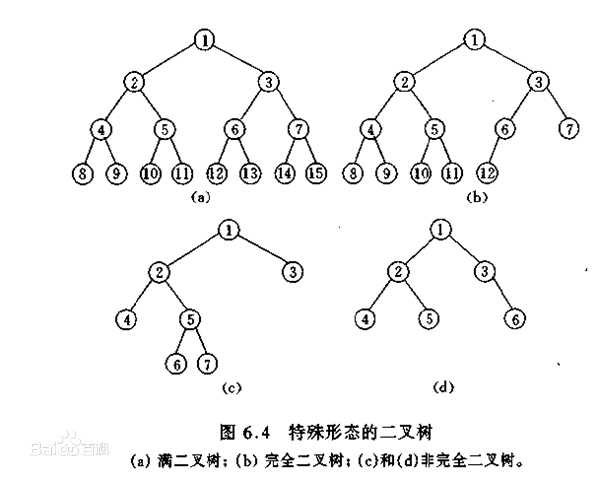
这就是一些简单的二叉树,这里A、B、C等我们成为节点。A叫做根节点,它的两个分支是B和C,并且我们称B是一个左子树,C是一个右子树,知道了这些简单的概念,我们就可以初步的探讨一些问题了。
二叉树树作为一种特殊的图,我们也要研究其遍历的方式,正如我们研究一般的图的遍历方式。由于其基本结构包括根、左子树、右子树,所以我们遍历的时候可以改变这三个元素的输出方式来得到不同的遍历顺序。
前序遍历的递归定义:对于一个节点,访问并输出根的信息;按照前序遍历左子树;按照前序遍历右子树。
中序遍历的递归定义:对于一个节点,按照中序遍历左子树;访问输出根的信息;按照中序遍历右子树。
后序遍历的递归定义:对于一个节点,按照后序遍历左子树;按照后序遍历右子树;访问并输出根的信息。
拿上图d举个例子,前序遍历:124536,;中序遍历:425361;后序遍历:452631。
值得注意的是,除了中序遍历,其余两种遍历方式可以推广到k叉树,因为对于中序遍历,每当遍历完左子树,都会访问一次根节点,这样会造成多次重复访问根节点,就谈不上“遍历”这二字了。
而且对于一个给定前(后)序遍历和中序遍历的二叉树,是可以唯一确定的。
那么我们来看一道关于二叉树这三种遍历的题目(Problem source :pku2255)

题目大意:给出一个二叉树的前序遍历、中序遍历,让你输出其后序遍历。
数理分析:根据其定义,三种遍历方式是通过递归生成的,那么现在知道了两种遍历方式,也是可以还原出原来的二叉树的。
举个例子,拿第一组数据来说,前序遍历为DBACEGF,中序遍历为ABCDEFG,那么我们通过前序遍历的定义,可知D是最大的那棵树的根,此时我们再通过中序遍历,ABC在D的左端,是左子树,而EFG在D的右端,为右子树,这样可以初步画一个树。然后我们在找前序遍历的第二个点……最终一定会还原出原来的二叉树。
这里题目要求直接输出后序遍历,那么我们在还原二叉树的同时也能构造出后序遍历。在起始情况中,前序遍历的第一个点作为整棵树的根,是要作为后序遍历的最后一个点的,这是我们再通过中序遍历和前序遍历找到此根下的右子树,我们把右子树看成一个整体,通过前序遍历又能找到一个根,再通过此根和中序遍历,分出左子树和右子树……直到这个根没有子树。
随后构造左子树。
这里之所先找根再找右子树在找左子树,是和后序遍历的递归概念呼应的。
编程实现:通过以上的描述,构造过程本质上是一种递归,也可以说是遍历图我们所熟悉的深搜。
参考代码如下。
#include<iostream> #include<string.h> using namespace std; char preorder[30]; char midorder[30]; char postorder[30]; int len; void travel(int preStar,int preEnd ,int midStar , int midEnd) { if(preStar > preEnd) return; postorder[--len] = preorder[preStar]; //记录根 if(preStar == preEnd) return; int i; for(i = 0;i <= midEnd;i++) if(midorder[i] == preorder[preStar]) break; travel(preStar + i - midStar + 1,preEnd, i + 1, midEnd); //左子树 travel(preStar + 1 , preStar + i - midStar , midStar , i - 1);//右子树 } int main() { while(cin>>preorder>>midorder) { len = strlen(preorder); postorder[len] = ‘\0‘; travel(0,len-1,0,len-1); cout << postorder<<endl; } }
我们这里下面将介绍一些树形结构在储存信息方面的一些其他应用。
首先我们介绍线段树。
线段树,顾名思义,一定是和线段有关的,我们通过一条线段[1,n]上的整数点储存信息,然后通过二分的方法形成完全二叉树来储存这些信息,并且还可以进行访问查找、更新数据等一系列操作,在后面具体问题的分析中我们都将讨论到。
线段树能够解决很多的问题,这里我们从一个简单的问题来入门线段树的学习——求指定区间的最大值问题。(Problem source : hdu1754)
题目大意很明了,数理分析也没有难度,那么这里我们重点分析它的编程实现。
我们先将整个问题进行功能划分,然后再考虑函数模块化的实现。在上述问题中,我们要完成数据的存储、访问数据得到最大值、更新数据。
这里也许人们会考虑直接用数组进行记录然后遍历求最大值,但是这种方法,第一,暴力穷举时间复杂度太高;第二,这种方法是很难完成对数据的更新。所以这里我们考虑构造线段树。
数据的存储:也就是我们说的建立一棵树。这里我们将用二分加深搜(dfs)进行构造,并在每个非叶节点记录其左子树和右子树的最大值,这里是通过深搜后再回溯来实现的。此时,我们若将n个人的分数看做线段[1,n]上整数的“携带”的信息,那么整棵树构造完成后,每个非叶节点都记录着某个区间段上的最大值。
访问数据得到最大值:这里我们依然需要采用二分的查找思想,然后将所求区间与我们构造出的线段树记录的信息进行匹配,得到答案。
更新数据:这里依然基于二分查找(因为构造线段树的时候就是用的二分法,这与我们所构造的线段是本质上是完全二叉树是呼应的),一旦找到所在的叶节点,便进行数据的更新,然后进行和建树时一样的回溯操作把整个书的节点都要更新一遍。
有了以上对编程过程的分析,再理解代码就不困难了。
参考代码如下。(代码中又>>和<<操作,无非是/2或*2,这里是为了得到线段树在对应的数组里的下标,读者稍微模拟一下就可以知道代码中为什么要这么写)。
#include<cstdio> #include<cmath> using namespace std; int Max[4000001]; int max(int a , int b) { return a>b?a:b; } void Pushup(int index) //回溯构造线段树 { Max[index] = max(Max[index<<1],Max[(index<<1)+1]); } void build(int l,int r,int index) //建立线段树 { if(l == r) { scanf("%d",&Max[index]); return; } int m = (l + r)>>1; build(l,m,index<<1); build(m+1,r,(index<<1)+1); Pushup(index); } void update(int p,int q,int l,int r,int index)//更新数据 { if(l == r) { Max[index] = q; return; } int m = (r+l)>>1; if(p <= m ) update(p,q,l,m,index<<1); else update(p,q,m+1,r,(index<<1)+1); Pushup(index); } int getMax(int L,int R,int l,int r,int index)//访问给定区间的数据 { if(L<=l && R >= r) return Max[index]; int m = (r+l)>>1; int ret = 0; if(L <= m) ret = max(ret,getMax(L,R,l,m,index<<1)); if(R > m) ret = max(ret,getMax(L,R,m+1,r,(index<<1)+1)); return ret; } int main() { int n , m , a , b , i; char c; while(scanf("%d%d",&n,&m) != EOF) { build(1,n,1); for(i = 0;i < m;i++) { scanf("%*c%c%d %d",&c,&a,&b); if(c == ‘Q‘) printf("%d\n",getMax(a,b,1,n,1)); else update(a,b,1,n,1); } } }
基于在《图论及其应用——图》中对于并查集简单的了解,这里我们将继续讨论一下关于“树”的问题。首先这里引入一些概念。
所谓生成树,简单的来说就是对于连通分量为1的Graph图——G(V,E),我们找到一个G的子图T(V‘,E‘),这里V = V‘,E‘ 则可以是E的子集。
那对应的生成森林,就是连通分量为n的Graph图,我们分别分析每一个连通分量,分别得到生成树,最后组在一起就成了生成森林。
而所谓的最小生成树,就是如果给定的Graph图——G(V,E)的点集E是带权值的(即这个边上存着数值),在所有生成树中,权值最小的那个即是最小生成树。
以上的定义显得很抽象,我们结合具体的问题来看就会更加明白。
那我们就拿来一个具体的例子来分析。(Problem source : hdu 1301)

题目大意:通过键盘输入给你一个Graph图——G(V,E),其中边集E是带权值的(就说连接点之间的边上储存着数值),现在你找到一个子图,要求这个子图能够连通原图中的所有点(也就是说这个图首先是原图的生成树),并且这个生成树的权值是所有生成树中最小的,即最小生成树。 数理分析:关于生成最小生成树的算法,常见的有prim算法和Kruskal算法,这里我们将介绍Kruskal算法。
它的具体步骤如下。
1.我们设G(V,E)是原图(点集V含有n个元素),G‘(V‘,E‘)是最小生成树。我们先将带权值的边集E进行排序。
2.我们先生成G‘(V,∅),然后从权值最小的边开始尝试构建最小生成树G‘,如果添加当前这条最小边导致生成了环,则弃掉当前边。
3.遍历所有的边,如果能够选出n - 1条,则说明得到了最小生成树,否则的话,只能生成最小森林。
Kruskal算法基于贪心的思想。为了得到生成树,我们要在边集E中选出n - 1个元素,这是保证含有n个元素的点集连通的最小边数,那么我们只需从最小的带权边开始构造即可。这个构造过程中,如果出现了某个边使生成树出现了环,那么我们至少需要n条边才能构造出生成树(这显而易见)。此时我们有两个选择,一种选择是,弃掉这条边,我们构造n-1个元素的边集V‘,另一种选择是,拿这条边,构造n个元素的边集V‘。我们简单的进行比较就能够的出答案。 E = {E1,E2,E3,E4,E5,E6}(按权值的递增排列)这里我们假设E3处生成环。
方案一:E1,E2,E4,E5。
方案二:E1,E2,E3,E4,E5,E6.(因为选择了导致构成环的E3对生成树的连通性没有影响,所以E3后面的点和方案一完全一样,但是要多一个元素) 显而易见,方案一才是运用了贪心思想的最优构造方法。 以上就是生成最小生成树的Kruskal算法。
编程实现:有了以上对Kruskal算法的理解再加上对并查集的理解,我们在编程实现上并不难实现它。 值得一提的是,在并查集和最小生成树一类的问题当中,往往是把本质上是无向的Graph图当做有向图来处理,这里主要是为了编程实现的方便。
参考代码如下。
#include<stdio.h> #include<string.h> using namespace std; int root[30]; int Find(int t) { if(root[t] == t) return t; else return root[t] = Find(root[t]); } void bing(int x,int y) { if(Find(x) != Find(y)) { if(Find(x) < Find(y)) root[Find(y)] = Find(x); else root[Find(x)] = Find(y); } } int main() { int n,i,j,k,x,y,Min,sum,cost[30][30]; char ch1,ch2; while(scanf("%d",&n) , n) { getchar(); memset(cost , -1 , sizeof(cost)); for(i = 1;i < n;i++) { root[i] = i; scanf("%c %d",&ch1,&k); for(j = 1;j <= k;j++) { scanf(" %c %d",&ch2,&x); cost[i][ch2 - ‘A‘ + 1] = x; } getchar(); } root[n] = n; sum = 0; for(k = 1;k < n;k++) { Min = 100000; for(i = 1;i < n;i++) { for(j = i + 1;j <= n;j++) { if(cost[i][j] > 0 && Find(i) != Find(j) && cost[i][j] < Min) { Min = cost[i][j]; x = i , y = j; } } } bing(x , y); sum += Min; } printf("%d\n",sum); } return 0; }
标签:
原文地址:http://www.cnblogs.com/rhythmic/p/5205702.html