标签:
求sigma(i : 1 to n)i^k。
为了做这个题这两天真是补了不少数论, 之前连乘法逆元都不知道...
关于拉格朗日插值法, 我是看的这里http://www.guokr.com/post/456777/, 还挺有趣...
根据题目给出的例子我们可以发现, k次方的通项公式的最高次是k+1次, 根据拉格朗日插值法, 构建一个k+1次的方程需要k+2项。
然后公式是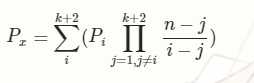 , 对于这个题, p[i]就是i^k+(i-1)^k+(i-2)^k+.....+1^k, 这部分可以预处理出来。 自己不会搞公式 , 从http://www.cnblogs.com/qscqesze/p/5207132.html这里盗的(雾
, 对于这个题, p[i]就是i^k+(i-1)^k+(i-2)^k+.....+1^k, 这部分可以预处理出来。 自己不会搞公式 , 从http://www.cnblogs.com/qscqesze/p/5207132.html这里盗的(雾
我们发现上面就是(n-1)*(n-2)......*(n-k-2)/(n-i), 上面的那部分预处理出来, 除(n-i)相当于乘(n-i)的乘法逆元。
下面那部分就是(i-1)*(i-2)*...(i-i+1) * (i-i-1)*(i-i-2)*......(i-k-2), 相当于两个阶乘相乘, 阶乘预处理出来, 然后注意一下后面的正负号就可以了。
#include <iostream> #include <vector> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <map> #include <set> #include <string> #include <queue> #include <stack> #include <bitset> using namespace std; #define pb(x) push_back(x) #define ll long long #define mk(x, y) make_pair(x, y) #define lson l, m, rt<<1 #define mem(a) memset(a, 0, sizeof(a)) #define rson m+1, r, rt<<1|1 #define mem1(a) memset(a, -1, sizeof(a)) #define mem2(a) memset(a, 0x3f, sizeof(a)) #define rep(i, n, a) for(int i = a; i<n; i++) #define fi first #define se second typedef pair<int, int> pll; const double PI = acos(-1.0); const double eps = 1e-8; const ll mod = 1e9+7; const int inf = 1061109567; const int dir[][2] = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} }; const int maxn = 1e6+5; ll f[maxn], fac[maxn]; ll pow(ll a, ll b) { ll ret = 1; while(b) { if(b&1) ret = (ret*a)%mod; a = (a*a)%mod; b>>=1; } return ret; } int main() { ll n, k; cin>>n>>k; for(int i = 1; i<=k+2; i++) { f[i] = (f[i-1]+pow(i*1LL, k))%mod; } fac[0] = 1; for(int i = 1; i<maxn; i++) { fac[i] = (fac[i-1]*i)%mod; } if(n<=k+2) { cout<<f[n]<<endl; return 0; } ll cur = 1, ans = 0; for(int i = 1; i<=k+2; i++) { cur = (cur*(n-i))%mod; } for(int i = 1; i<=k+2; i++) { ll tmp = pow(n-i, mod-2)%mod; ll tmp1 = pow(fac[i-1]%mod*fac[k+2-i]%mod, mod-2)%mod; int sign = (k+2-i)%2?-1:1; ans = (ans + sign*tmp*tmp1%mod*f[i]%mod*cur%mod)%mod; } ans = (ans+mod)%mod; cout<<ans<<endl; return 0; }
codeforces 622F. The Sum of the k-th Powers 拉格朗日插值法
标签:
原文地址:http://www.cnblogs.com/yohaha/p/5218291.html