标签:
RMQ:范围最小值问题。给出一个n个元素的数组A1,A2,...,An,设计一个数据结构支持查询操作Query(L,R):计算min{AL,AL+1,...,AR}。
每次用一个循环来求最小值显然不够快快,前缀和的思想也不能提高效率,这时候ST算法就派上用场了,它预处理的时间是O(nlogn),但是查询只需要Q(1),而且常数很小。
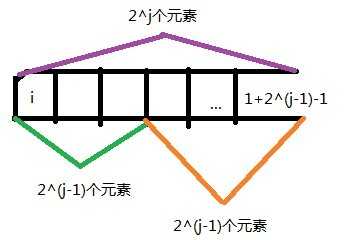
令dp[i][j]表示从i开始的,长度为2^j的一段元素中的最小值,递推公式:dp[i][j]=min{dp[i][j-1],dp[i+2^(j-1)][j-1]}
模板代码:
void RMQ_init(const vector<int> &A) { int n=A.size(); for(int i=0;i<n;++i) d[i][0]=A[i]; for(int j=1;(1<<j)<=n;++j) //长度 for(int i=0;i+(1<<j)-1 <= n;++i) //起点,虽然书上写的是 < n d[i][j]=min(d[i][j-1],d[i+(1<<(j-1))][j-1]); } int RMQ(int L,int R) { int k=0; while((1<<(k+1))<=R-L+1) k++; //int k=(int)((log(R-L+1))/log(2.0)); return min(d[L][k],d[R-(1<<k)+1][k]); }
模板题:南阳理工119
题意:求一段区间内的最大值和最小值之差,所以统计最大值和最小值分别用RMQ来统计

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 const int Max = 100000 + 10; 7 int maxsum[Max][32],minsum[Max][32]; 8 int n,q,v; 9 void RMQ_init() 10 { 11 for(int j = 1; (1 << j) <= n; j++) 12 { 13 for(int i = 1; i + (1 << j) - 1 <= n; i++) 14 { 15 maxsum[i][j] = max(maxsum[i][j - 1], maxsum[i + (1 << (j - 1))][j - 1]); 16 minsum[i][j] = min(minsum[i][j - 1], minsum[i + (1 << (j - 1))][j - 1]); 17 } 18 } 19 } 20 int RMQ(int l, int r) 21 { 22 int k = 0; 23 while( (1 << (k + 1)) <= (r - l + 1)) 24 k++; 25 int maxn = max(maxsum[l][k], maxsum[r - (1 << k) + 1][k]); 26 int minn = min(minsum[l][k], minsum[r - (1 << k) + 1][k]); 27 28 return maxn - minn; 29 } 30 int main() 31 { 32 while(scanf("%d%d", &n, &q) != EOF) 33 { 34 for(int i = 1; i <= n; i++) 35 { 36 scanf("%d", &v); 37 minsum[i][0] = maxsum[i][0] = v; 38 } 39 RMQ_init(); 40 while(q--) 41 { 42 int a,b; 43 scanf("%d%d", &a, &b); 44 printf("%d\n", RMQ(a,b)); 45 } 46 } 47 return 0; 48 }
标签:
原文地址:http://www.cnblogs.com/zhaopAC/p/5223224.html