标签:style blog http color 数据 2014 c 算法
B树
定义:一棵B树T是具有如下性质的有根树:
1)每个节点X有以下域:
a)n[x],当前存储在X节点中的关键字数,
b)n[x]个关键字本身,以非降序存放,因此key1[x]<=key2[x]<=...<=keyn[x][x],
c)leaf[x],是一个布尔值,如果x是叶子的话,则它为TRUE,如果x为一个内节点,则为FALSE。
2)每个内节点包含n[x]+1个指向其子女的指针c1[x],c2[x],...,cn[x]+1[x]。叶节点没有子女,故它们的ci域无意义。
3)各关键字keyi[x]对存储在各子树中的关键字范围加以分隔:如果ki为存储在以以ci[x]为根的子树中的关键字,则
ki<=key1[x]<=k2<=key2[x]<=...<=keyn[x]<=keyn[x]+1
4)每个叶结点具有相同的深度,即树高h。
5)每一个结点能包含的关键字树有一个上界和下界。这些界可以用一个称作B树的最小度数的固定值t>=2表示。
a)每个非根的结点必须至少有t-1个关键字。每个非根的内结点至少有t个子女。如果树是非空的,则根结点至少包含一个 关键字。
b)每个结点可包含最多2t-1个关键字,所以一个内结点至多可以有2t个子女。我们说一个结点是满的,如果它恰好有2t-1 个关键字。
t=2时B树是最简单的。这时每个内结点有2个、3个或4个子女,亦即一棵2-3-4树。然而在实际中,通常采用很大的t。
用途:
B树是为磁盘或其它辅助存储设备而设计的一种多路平衡查找树。
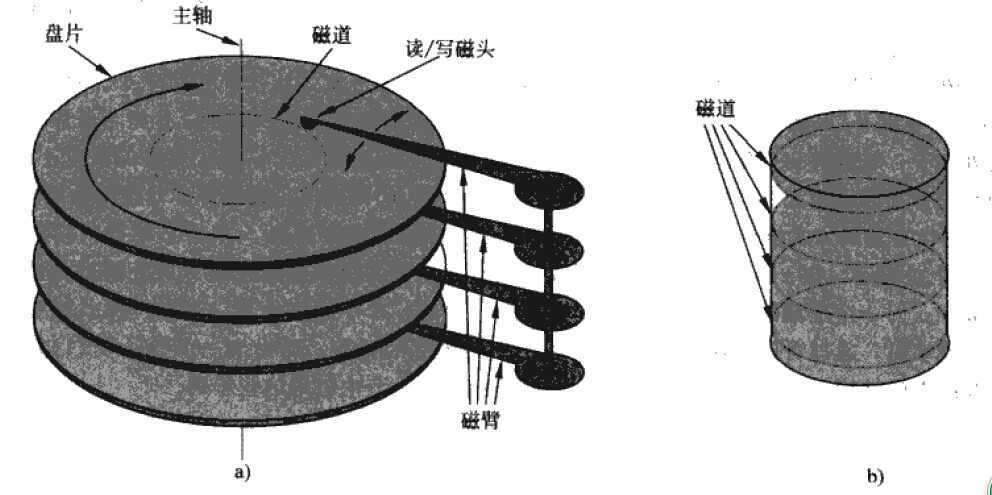
为什么针对磁盘设计的数据结构不同于这对随机存储器设计的数据结构?
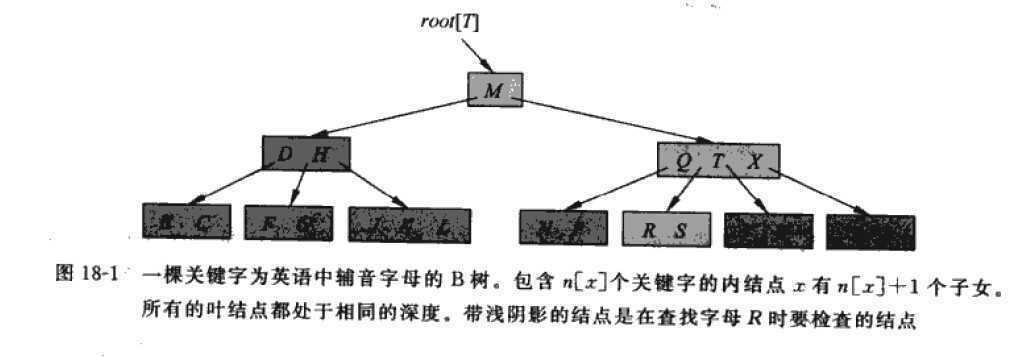
B树以自然的方式推广二叉查找树。如果B树的内结点X包含n[x]个关键字,则x就有n[x]+1个子女。结点X中的关键字是用来将X所处理的关键字域划分成n[x]+1个子域的分隔点,每个子域都有X中的一个子女来处理。当在一棵B树中查找某个关键字时,通过对存储在结点X中的n[x]个关键字的比较,而做出一个n[x]+1路的决定。叶节点的结构不同于内部结点的结构。
在一个典型的B树的应用中,要处理的数据量很大,因此无法一次都装入主存。B树算法将所需的页(“页”这个概念需要计算机组成原理和操作系统的知识)选择出来复制到主存中去,而后将修改过的页再写回到磁盘中去。因为在任何时刻,B树算法在主存中都只需要一定量的页数,故主存的大小并不限制可被处理的B树的大小。在B树中,一个结点的大小通常相当于一个完整的磁盘页。
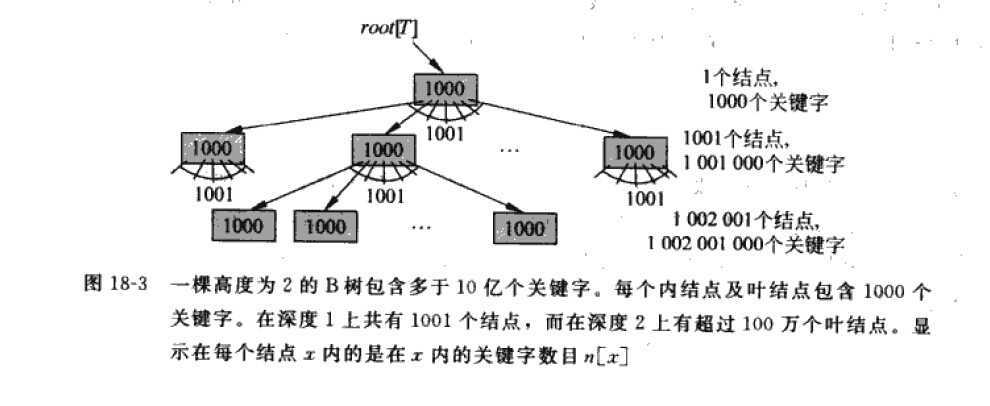
对存储在磁盘上的一棵大的B树,通常采用的分支因子为50到2000,具体要取决于关键字相对于一页的大小 。选取一个大的分支因子,可以大大降低数的高度,以及寻找任意关键字时所需的磁盘存取次数。上图显示了一棵分支因子为1001、高度为2的B树,它可以存储超过10亿个关键字;尽管如此,根节点还是可以持久的保留在内存中,在这棵树中寻找某一关键字至多需两次磁盘存取!
D&F学数据结构系列——B树(B-树和B+树)介绍,布布扣,bubuko.com
标签:style blog http color 数据 2014 c 算法
原文地址:http://www.cnblogs.com/sage-blog/p/3867777.html