Alice和Bob在图论课程上学习了最大流和最小费用最大流的相关知识。
最大流问题:给定一张有向图表示运输网络,一个源点S和一个汇点T,每条边都有最大流量。一个合法的网络流方案必须满足:(1)每条边的实际流量都不超过其最大流量且非负;(2)除了源点S和汇点T之外,对于其余所有点,都满足该点总流入流量等于该点总流出流量;而S点的净流出流量等于T点的净流入流量,这个值也即该网络流方案的总运输量。最大流问题就是对于给定的运输网络,求总运输量最大的网络流方案。
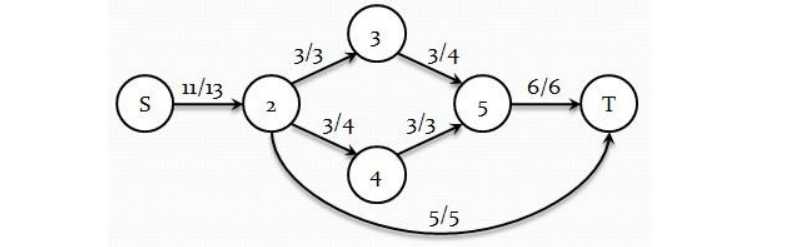
上图表示了一个最大流问题。对于每条边,右边的数代表该边的最大流量,左边的数代表在最优解中,该边的实际流量。需要注意到,一个最大流问题的解可能不是唯一的。 对于一张给定的运输网络,Alice先确定一个最大流,如果有多种解,Alice可以任选一种;之后Bob在每条边上分配单位花费(单位花费必须是非负实数),要求所有边的单位花费之和等于P。总费用等于每一条边的实际流量乘以该边的单位花费。需要注意到,Bob在分配单位花费之前,已经知道Alice所给出的最大流方案。现茌Alice希望总费用尽量小,而Bob希望总费用尽量大。我们想知道,如果两个人都执行最优策略,最大流的值和总费用分别为多少。
第一行三个整数N,M,P。N表示给定运输网络中节点的数量,M表示有向边的数量,P的含义见问题描述部分。为了简化问题,我们假设源点S是点1,汇点T是点N。
接下来M行,每行三个整数A,B,C,表示有一条从点A到点B的有向边,其最大流量是C。
第一行一个整数,表示最大流的值。
第二行一个实数,表示总费用。建议选手输出四位以上小数。
【样例说明】
对于Alice,最大流的方案是固定的。两条边的实际流量都为10。
对于Bob,给第一条边分配0.5的费用,第二条边分配0.5的费用。总费用
为:10*0.5+10*0.5=10。可以证明不存在总费用更大的分配方案。
【数据规模和约定】
对于20%的测试数据:所有有向边的最大流量都是1。
对于100%的测试数据:N < = 100,M < = 1000。
对于l00%的测试数据:所有点的编号在I..N范围内。1 < = 每条边的最大流
量 < = 50000。1 < = P < = 10。给定运输网络中不会有起点和终点相同的边。
1 #include<cmath>
2 #include<queue>
3 #include<vector>
4 #include<cstdio>
5 #include<cstring>
6 #include<iostream>
7 #include<algorithm>
8 #define FOR(a,b,c) for(int a=(b);a<=(c);a++)
9 using namespace std;
10
11 const int N = 105;
12 const double INF = 1e9;
13 const double eps = 1e-8;
14
15 struct Edge {
16 int u,v; double cap,flow;
17 };
18
19 struct Dinic {
20 int n,m,s,t,d[N],cur[N],vis[N];
21 vector<Edge> es;
22 vector<int> g[N];
23 queue<int> q;
24 void init(int n) {
25 this->n=n;
26 es.clear();
27 for(int i=0;i<=n;i++) g[i].clear();
28 }
29 void clear() {
30 for(int i=0;i<es.size();i++) es[i].flow=0;
31 }
32 void AddEdge(int u,int v,double w) {
33 es.push_back((Edge){u,v,w,0});
34 es.push_back((Edge){v,u,0,0});
35 int m=es.size();
36 g[u].push_back(m-2); g[v].push_back(m-1);
37 }
38 bool bfs() {
39 memset(vis,0,sizeof(vis));
40 vis[s]=1; d[s]=0; q.push(s);
41 while(!q.empty()) {
42 int u=q.front(); q.pop();
43 for(int i=0;i<g[u].size();i++) {
44 Edge& e=es[g[u][i]];
45 int v=e.v;
46 if(e.cap>e.flow && !vis[v]) {
47 vis[v]=1; d[v]=d[u]+1;
48 q.push(v);
49 }
50 }
51 }
52 return vis[t];
53 }
54 double dfs(int u,double a) {
55 if(u==t || fabs(a)<eps) return a;
56 double flow=0,f;
57 for(int& i=cur[u];i<g[u].size();i++) {
58 Edge& e=es[g[u][i]];
59 int v=e.v;
60 if(d[v]==d[u]+1 && (f=dfs(v,min(a,e.cap-e.flow)))>0) {
61 flow+=f; a-=f;
62 e.flow+=f;
63 es[g[u][i]^1].flow-=f;
64 if(fabs(a)<eps) break;
65 }
66 }
67 return flow;
68 }
69 double Maxflow(int s,int t) {
70 this->s=s; this->t=t;
71 double flow=0;
72 while(bfs()) {
73 memset(cur,0,sizeof(cur));
74 flow+=dfs(s,INF);
75 }
76 clear();
77 return flow;
78 }
79 } dc;
80
81 int n,m,p; double maxflow;
82
83 Edge te[N*N];
84 bool can(double M) {
85 for(int i=0;i<dc.es.size();i++)
86 te[i]=dc.es[i],dc.es[i].cap=min(dc.es[i].cap,M);
87 double ans=dc.Maxflow(1,n);
88 for(int i=0;i<dc.es.size();i++)
89 dc.es[i]=te[i];
90 return fabs(ans-maxflow)<eps;
91 }
92
93 int main() {
94 scanf("%d%d%d",&n,&m,&p);
95 dc.init(n);
96 int u,v; double w,L=0,R;
97 FOR(i,1,m) {
98 scanf("%d%d%lf",&u,&v,&w);
99 dc.AddEdge(u,v,w); R=max(R,w);
100 }
101 maxflow=dc.Maxflow(1,n);
102 while((R-L)>eps) {
103 double M=(L+R)*0.5;
104 if(can(M)) R=M; else L=M;
105 }
106 printf("%.0f\n%.4f",maxflow,(double)p*L);
107 return 0;
108 }

