标签:
一、残留网络及增广路
残留网络、增广路及割是构成最大流最小割定理的三个基本概念,该定理巧妙地运用网络中的最小割来描述最大流的值。
1.残留网络
对于网络G=(V,E,C),设流f是G中的流。残留网络直观上讲是由还可以容纳更多的流的边组成。对于G中的每条边<u,v>,可以定义残留容量为在不超过容量限制的条件下,可以通过的额外的网络流量
cf(u,v)=c(u,v)-f(u,v)
事实上,残留网络也是一个网络,容量由cf给出。设f是网络G=(V,E,C)的一个流,f1是残留网络Gf的一个流,则f+f1依然是网络G的一个流。这个引理给出了残留网络与原网络的关系,也为提出增广路1提供了前提。
2.增广路
定义:增广路p为残留网络Gf上的源s到汇t的一条简单路径。该路径的残留容量为可以沿该路径增加的最多额外流量:cf(p)=min{cf(u,v) | <u,v>∈p}。这个值是严格大于0的。
从上面的描述可以推导出增广路的可增广性质,定义流fp为
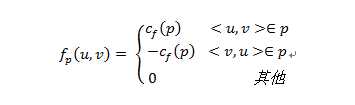
给定网络G中的一个流f,则f+fp依然是网络G的一个流。
二、最小割最大流定理
1.割
网络G=(V,E,C)中割[S,T]将点集V划分为S、T(S=V-T)两个部分,使得s∈S且t∈T。符号[S,T]代表边集合{<u,v>| <u,v>∈E, u∈S, v∈T}。穿过割[S,T]的净流定义为f(S,T),割[S,T]的容量定义为c(S,T)。一个网络的最小割也就是该网络中的容量最小的割。
2.最小割最大流定理
可以完整描述最小割最大流定理如下:
如果f是具有源s和汇t的网络G={V,E,C}中的一个流,则下列条件是等价的:
(1)f是G的一个最大流;
(2)残留网络Gf不包含增广路径;
(3)对G的某个割[S,T],有|f|=c(S,T)。
三、最大流算法
1.Ford-Fulkson方法的基本思想
Ford-Fulkson(简称FF)方法是由Ford和Fulkson两位数学家发明的。充分利用最小割最大流定理,并创造性地发明了回退边,使得增广成为一种动态修改的过程,并且保证了最终结果的正确性。
FF方法的具体步骤:
(1)初始化网络中所有边的容量,c<u,v>继承该边的容量,c<v,u>初始化为0,其中边<v,u>即为回退边。初始化最大流为0。
(2)在残留网络中找一条从源S到汇T的增广路p。如能找到,则转步骤(3);如不能找到,则转步骤(5)。
(3)在增光路p中找到所谓的“瓶颈”边,即路径中容量最小的边,记录下这个值X,并且累加到最大流中,转步骤(4)。
(4)将增广路中所有c<u,v>减去X,所有c<v,u>加上X,构成新的残留网络。转步骤(2)。
(5)得到网络的最大流,退出。
《算法导论》中严格定义FF方法为一种方法而非算法,也许正是因为FF方法中的第(2)步并未给出具体的寻找增广路方法。寻找增广路方法的不确定导致
标签:
原文地址:http://www.cnblogs.com/WCB-ACM/p/5233367.html