标签：存储   printf   64位   杭电   递推   

彼岸

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2909    Accepted Submission(s): 1604

突破蝙蝠的包围，yifenfei来到一处悬崖面前，悬崖彼岸就是前进的方向，好在现在的yifenfei已经学过御剑术，可御剑轻松飞过悬崖。
现在的问题是：悬崖中间飞着很多红，黄，蓝三种颜色的珠子，假设我们把悬崖看成一条长度为n的线段，线段上的每一单位长度空间都可能飞过红，黄，蓝三种珠子，而yifenfei必定会在该空间上碰到一种颜色的珠子。如果在连续3段单位空间碰到的珠子颜色都不一样，则yifenfei就会坠落。
比如经过长度为3的悬崖，碰到的珠子先后为 “红黄蓝”，或者 “蓝红黄” 等类似情况就会坠落，而如果是 “红黄红” 或者 “红黄黄”等情况则可以安全到达。
现在请问：yifenfei安然抵达彼岸的方法有多少种？

2
2
3

9
21

这道题又是 递推的问题：

思路如下：

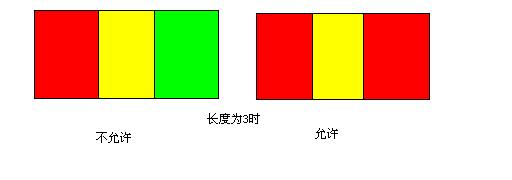
要想判断数为N的情况，需要判断n-1是什么颜色

则需要看f(n-1)与f(n-2)是否颜色相同

若颜色相同 则有f(n-2)种排列

若颜色不同 则有 f(n-1)-f(n-2)种排列

然后对 第N项

则有 当颜色相同的时候 因为有三种颜色可以选择 故共有

f(n-2)*3种可能

当颜色不同的时候 因为只剩下两种选择 故共有 2*(f(n-1)-f(n-2))种可能

所以有下面等式

f(n)=f(n-2)*3+2*(f(n-1)-f(n-2))=2*f(n-1)+f(n-2)

#include<stdio.h>
int main()
{
 int n,i,a;

 __int64 b[66]={0,3,9};
 for(i=3;i<66;i++)
 {
  b[i]=2*b[i-1]+b[i-2];
 } 
 scanf("%d",&n);
 while(n--)
 {
  scanf("%d",&a);
  printf("%I64d\n",b[a]);
 }
 return 0;
}

杭电 2569,布布扣,bubuko.com

杭电 2569

标签：存储   printf   64位   杭电   递推   

原文地址：http://blog.csdn.net/ice_alone/article/details/38118803