标签：
我们知道线性回归模型有一些适用条件：1.线性、2.无自相关、3.残差符合正态分布、4.方差齐性。当数据无法满足这些条件时，我们要么对数据进行转换，使之符合线性回归的条件，要么对模型进行调整，使之适应原始数据。总之，这是一个数据和模型相互适应的过程。下面我们分别来介绍一下，当这四种条件不满足时的处理方法：
一、非线性情况
线性回归模型的最重要的一个前提条件是，数据呈线性趋势，这点可以通过实现做散点图或拟合完成之后做残差图来进行判断，当数据不符合线性趋势时，可以采用两种方法进行处理
1.变量线性化
基本思路是先确定函数类型，然后通过线性变换，使其呈线性趋势。确定函数类型，可以根据专业知识、文献、经验等进行确定，也可以观察散点图，当有不止一种类型可以选择时，可以多做几次回归进行比较，选择最优者。确定了函数类型之后，就可以进行变换了，例如：
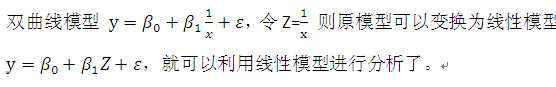
下面是一些常见的函数类型及其变换关系
变量变换方法对于函数关系明确时非常方便，但是缺点也很明显：
1.并非所有的函数类型都可以进行线性变换
2.当有不止一种类型可以选择时，确定起来很麻烦，并且如果选择错误，虽然线性变换和回归还是可以照常进行，但是最终的结果是错误的。
3.线性回归使用的是最小二乘法拟合，虽然变量变换之后可以保证残差平方和最小，但是对于原始数值来讲，并不一定是最优方程。
2.非线性回归模型
鉴于变量线性化的局限，可以直接使用非线性回归，非线性回归的参数估计和线性回归类似，也是先给出一个估计误差的函数(或称为损失函数)，然后使得该函数最小化，取得此时的参数值。
由于方程是非线性的，无法直接计算出最小二乘法估计出的参数值，一般采用高斯-牛顿法进行估计，这一方法是对非线性方程做泰勒级数展开，使非线性方程在某一初始值近似线性化，然后对其使用最小二乘法进行参数估计，并且将估计出的参数值带入方程，再进行泰勒级数展开，再对近似线性化的方差使用最小二乘法进行参数估计，如此反复，直到参数估计值收敛为止。
注意，初始值的设定对回归结果影响很大，要慎重设定初始值。
=======================================================
二、方差不齐的情况
方差齐性也是线性模型的基本假设之一，说的是整个分析过程中随机误差的方差为一个定值，不随自变量变化而变化，但是实际分析中经常遇到总体方差不是固定常数，而是变化的，这就是方差不齐的情况，也称为异方差性。
首先来说一下异方差性
异方差主要存在于横截面数据中，产生的原因有：
1.被解释变量的测量误差随时间而变化
2.存在某些被忽略的解释变量
3.模型的数学形式错误
4.数据为分组数据
5.某些的经济行为
异方差可以归为三种类型
1.单调递增：方差随X增大而增大
2.单调递减：方差随X增大而增大
3.复杂：无明显规律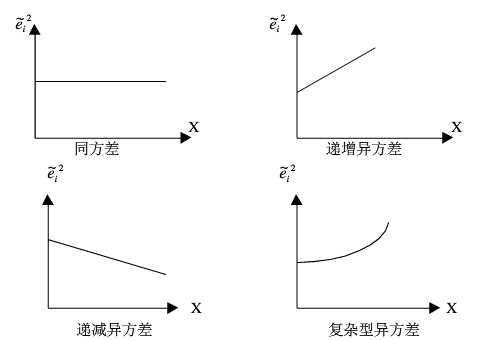
出现异方差时，如果仍然使用普通最小二乘法进行参数估计，会出现以下问题
1.估计出的参数不具有有效性
虽然还是无偏的，但是不具有有效性，因为在有效性证明中，假定了方差为定值
2.变量的显著性检验失去意义
因为变量显著性检验构造的t统计量，也是方差不变的基础上，其他检验也是如此
3.模型预测失效
因为预测值的置信区间中也包含了参数方程的估计量，这个值已经不准确，那么置信区间也不会准确了。
总之，异方差出现时，任何基于方差恒定而推断出的信息都将失效，并且会造成对Y的预测误差变大，预测精度降低。
异方差的判断方法：
既然异方差是对于不同的观测值随机误差具有不同的方差，那么判断异方差性就直接检验随机误差项的方差与变量观测值之间的相关性及相关形式如何即可
1.图示法
制作方差-随机误差项的散点图，看是否为一条斜率为0的直线
2.帕克-格里瑟检验
建立一个随机误差和变量观测值之间的方程，如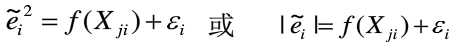
选择关于变量X的不同函数形式，对方程进行估计并进行显著性检验，如果存在某一种函数形式使得方程显著成立，则说明原模型存在异方差性，常用的函数形式如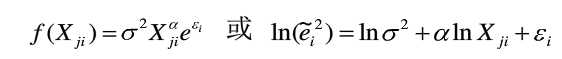
如果α在统计上是显著的，说明存在异方差性
3.格德菲尔德-匡特检验（G-Q检验）
以F检验为基础，先将样本按观测值大小排序并一分为二，对样本1和样本2分别做回归，然后利用两个样本的残差平方和之比构造的统计量进行检验。该统计量服从F分布，如果存在递增异方差，则F大于1，递减异方差F小于1，同方差F=1。
步骤1：对n个样本按照观测值大小排序
步骤2：将序列中间的c=n/4个观测值除去，并将剩余的观测值划分为较小与较大的相同的两个子样本，每个子样本的样本容量均为(n-c)/2
步骤3：对每个子样本分别使用普通最小二乘法进行回归估计，并计算各自的残差平方和
步骤4：设定原假设为同方差，构造F统计量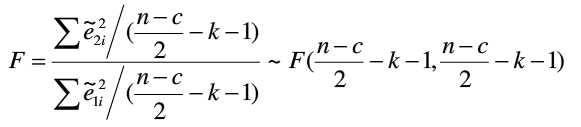
在给定显著性水平α条件下，确定临界值Fα，若F>Fα则拒绝原假设，说明存在异方差
4.怀特检验
先对模型做普通最小二乘法回归，得到一个残差平方和，然后对这个残差平方和进行回归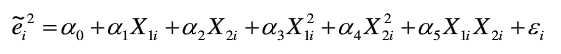
如果为同方差，则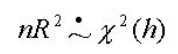
R2为残差平方和回归的可决系数，h为解释变量的个数，中间的符号表示为渐近分布
异方差的修正
前面说过异方差出现时不宜再使用普通最小二乘法，可以改用加权最小二乘法WLS进行估计。加权最小二乘法是对原模型进行加权处理，对较小的残差平方赋予较大的权重，对较大的残差平方赋予较小的权重，这样可以消除其异方差性，然后再使用普通最小二乘法进行参数估计。例如：
某个数据模型，经检验得知：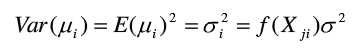
可以看出该模型方差随着X变化而变化，存在异方差性，那么我们用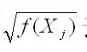
去除该模型，得到新的模型，
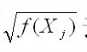也被称为权重函数
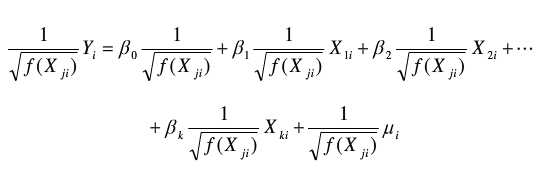
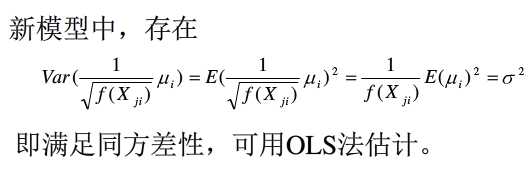
对原有的模型乘以权数，然后再做普通最小二乘法，这就是加权最小二乘法，这里的权数就是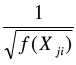
，据此得到的估计量也是无偏、有效的，但这只是理论上的最优权重函数，在实际分析中，最优权重函数往往是未知的，只能根据经验去假设，因此得到的加权最小二乘估计只能是近似的无偏。
总之，加权最小二乘法是解决异方差性的一种常用方法，但并非唯一的方法，并且加权最小二乘法权重函数的选择很重要，会直接影响到分析结果，权重函数的确定，目前没有统一的标准和方法，每个模型都有自己独有的最佳权重函数，有时甚至需要多个权重函数进行比较，从中选择最优者。一些统计软件如SPSS也有默认权重函数，在需要人工确定时，有人提出将普通最小二乘法得到的残差方差和变量x确定一条抛物线，用此作为权重函数。也有人提出使用迭代算法来进行加权等，对此还需进一步探讨。
标签：
原文地址：http://www.cnblogs.com/xmdata-analysis/p/5256965.html
