标签:
在我们的现实生活中,许多复杂系统都可以建模成一种复杂网络进行分析,比如常见的电力网络、航空网络、交通网络、计算机网络以及社交网络等等。复杂网络不仅是一种数据的表现形式,它同样也是一种科学研究的手段。复杂网络方面的研究目前受到了广泛的关注和研究,尤其是随着各种在线社交平台的蓬勃发展,各领域对于在线社交网络的研究也越来越火。研究生期间,本人的研究方向也是一直与复杂网络打交道,现在马上就要毕业了,写一篇博文简单介绍一下复杂网络特点以及一些有关复杂网络研究内容的介绍,希望感兴趣的博友可以一起讨论,一起学习。
下图分别是一个航空网络(上图)和Facebook网络全球友谊图(下图)。
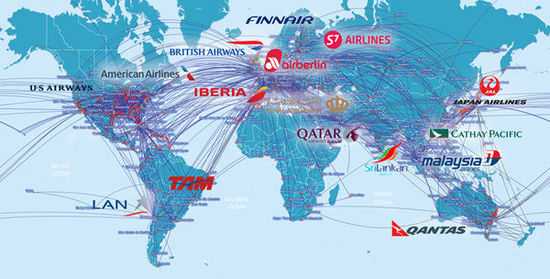
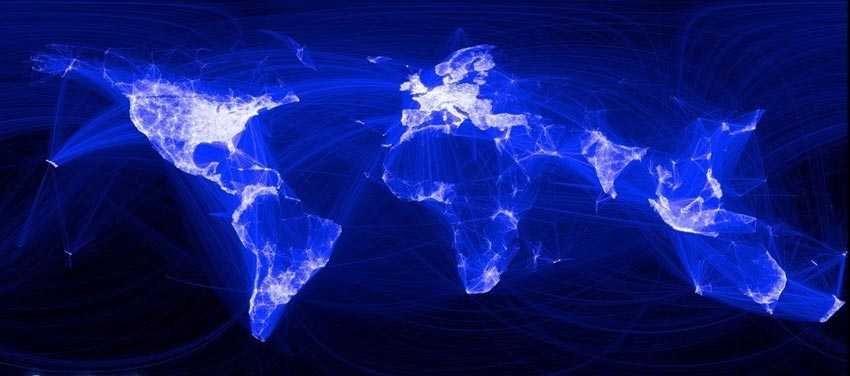
钱学森对于复杂网络给出了一种严格的定义:具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称之为复杂网络。言外之意,复杂网络就是指一种呈现高度复杂性的网络,其特点主要具体体现在如下几个方面:
小世界特性(Small world theory)又被称之为是六度空间理论或者是六度分割理论(Six degrees of separation)。小世界特性指出:社交网络中的任何一个成员和任何一个陌生人之间所间隔的人不会超过六个,如下图所示:
现实世界的网络大部分都不是随机网络,少数的节点往往拥有大量的连接,而大部分节点却很少,节点的度数分布符合幂率分布,而这就被称为是网络的无标度特性(Scale-free)。将度分布符合幂律分布的复杂网络称为无标度网络。
下图为一个具有10万个节点的BA无标度网络的度数分布示意图:
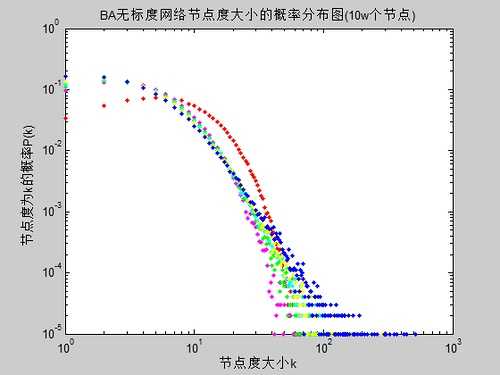
无标度特性反映了复杂网络具有严重的异质性,其各节点之间的连接状况(度数)具有严重的不均匀分布性:网络中少数称之为Hub点的节点拥有极其多的连接,而大多数节点只有很少量的连接。少数Hub点对无标度网络的运行起着主导的作用。从广义上说,无标度网络的无标度性是描述大量复杂系统整体上严重不均匀分布的一种内在性质。
其实复杂网络的无标度特性与网络的鲁棒性分析具有密切的关系。无标度网络中幂律分布特性的存在极大地提高了高度数节点存在的可能性,因此,无标度网络同时显现出针对随机故障的鲁棒性和针对蓄意攻击的脆弱性。这种鲁棒且脆弱性对网络容错和抗攻击能力有很大影响。研究表明,无标度网络具有很强的容错性,但是对基于节点度值的选择性攻击而言,其抗攻击能力相当差,高度数节点的存在极大地削弱了网络的鲁棒性,一个恶意攻击者只需选择攻击网络很少的一部分高度数节点,就能使网络迅速瘫痪。
人以类聚,物以群分。复杂网络中的节点往往也呈现出集群特性。例如,社会网络中总是存在熟人圈或朋友圈,其中每个成员都认识其他成员。集群程度的意义是网络集团化的程度;这是一种网络的内聚倾向。连通集团概念反映的是一个大网络中各集聚的小网络分布和相互联系的状况。例如,它可以反映这个朋友圈与另一个朋友圈的相互关系。
下图为网络聚集现象的一种描述:
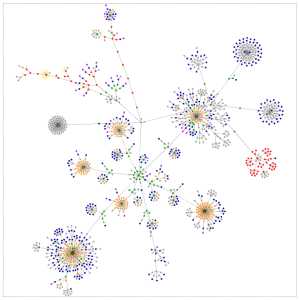
社区检测(community detection)又被称为是社区发现,它是用来揭示网络聚集行为的一种技术。社区检测实际就是一种网络聚类的方法,这里的“社区”在文献中并没有一种严格的定义,我们可以将其理解为一类具有相同特性的节点的集合。近年来,社区检测得到了快速的发展,这主要是由于复杂网络领域中的大牛Newman提出了一种模块度(modularity)的概念,从而使得网络社区划分的优劣可以有一个明确的评价指标来衡量。一个网络不通情况下的社区划分对应不同的模块度,模块度越大,对应的社区划分也就越合理;如果模块度越小,则对应的网络社区划分也就越模糊。
下图描述了网络中的社区结构:
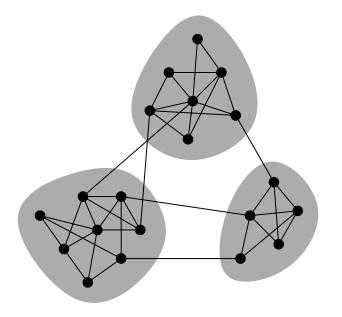
Newman提出的模块度计算公式如下:
[Math Processing Error]
其中[Math Processing Error]为网络中总的边数,[Math Processing Error]是网络对应的邻接矩阵,[Math Processing Error]代表节点[Math Processing Error]和节点[Math Processing Error]之间存在连边,否则不存在连边。[Math Processing Error]为节点[Math Processing Error]的度数,[Math Processing Error]为节点[Math Processing Error]属于某个社区的标号,而[Math Processing Error]当且仅当[Math Processing Error]。
上述的模块度定义其实很好理解,我们可以根据一个网络的空模型去进行理解。网络的空模型可以理解为只有节点的而没有连边,这时候一个节点可以和图中的任意其他节点相连,并且节点[Math Processing Error]和[Math Processing Error]相连的概率可以通过计算得到。随机选择一个节点与节点[Math Processing Error]相连的概率为[Math Processing Error],随机选择一个节点与节点[Math Processing Error]相连的概率为[Math Processing Error],那么节点[Math Processing Error]和节点[Math Processing Error]相连的概率为[Math Processing Error],边数的期望值[Math Processing Error]。所以模块度其实就是指一个网络在某种社区划分下与随机网络的差异,因为随机网络并不具有社区结构,对应的差异越大说明该社区划分越好。
Newman提出的模块度具有两方面的意义:
(1)模块度的提出成为了社区检测评价一种常用指标,它是度量网络社区划分优劣的量化指标;
(2)模块度的提出极大地促进了各种优化算法应用于社区检测领域的发展。在模块度的基础之上,许多优化算法以模块度为优化的目标方程进行优化,从而使得目标函数达到最大时得到不错的社区划分结果。
当然,模块度的概念不是绝对合理的,它也有弊端,比如分辨率限制问题等,后期国内学者在模块度的基础上提出了模块度密度的概念,可以很好的解决模块度的弊端,这里就不详细介绍了。
常用的社区检测方法主要有如下几种:
(1)基于图分割的方法,如Kernighan-Lin算法,谱平分法等;
(2)基于层次聚类的方法,如GN算法、Newman快速算法等;
(3)基于模块度优化的方法,如贪婪算法、模拟退火算法、Memetic算法、PSO算法、进化多目标优化算法等。
结构平衡(Structural Balance)主要是针对社交网络的研究而被提出的,它最早源于社会心理学家Heider提出的一个结构平衡理论。
3.1 网络平衡的发展
网络平衡有时也称社会平衡(Social Balance),就网络平衡的发展来说,我们可以将其分为三个发展阶段。
3.1.1 网络平衡理论的提出
“网络平衡”一词最早是由Heider基于对社会心理学的研究而提出的,Heider在1946年的文章Attitudes and cognitive organization[1]中针对网络平衡的概念提出了最早的平衡理论:
(1)朋友的朋友是朋友;
(2)朋友的敌人是敌人;
(3)敌人的朋友是敌人;
(4)敌人的敌人是朋友。
用常见的三元组合来表示上述的Heider理论如下:
上述的平衡理论是有关网络平衡提出的最早的理论,它后来也被称为是强平衡理论。
1956年,Cartwright和Harary对Heider的平衡理论进行了推广,并将其用在了图理论中(STRUCTURAL BALANCE: A GENERALIZATION OF HEIDER‘S THEORY[2])。Cartwright和Harary指出对于一个符号网络而言,网络平衡的充要条件是网络中的所有三元组都是平衡的,该结论也可以陈述为一个符号网络平衡的充要条件是它所包含的所有回路(cycles)都是平衡的(“-”号的个数为整数个)。而且,在这篇文章中,他们还提出了著名的结构平衡理论:如果一个符号网络是平衡的,那么这个网络就可以分为两部分子网络,其中每个子网络内部中节点的连接都是正连接,网络之间的连接均为负连接。
在这各阶段网络平衡的发展的重心主要在于构建网络平衡的心理学和社会学模型。
3.1.2 网络平衡的数学模型
在有了Heider等人的奠基工作后,有关网络平衡的发展主要是构建其数学模型,比如网络的动态表现,一个网络连接如何随时间的变化而变化,网络中节点之间的朋友或者敌人的关系如何演化等等。
3.1.3 网络平衡的应用
最新关于网络平衡方面的研究大都是研究一些在线网络,比如对某个网站用户属性的分析等等。而且,目前我们身处大数据时代,我们所要研究的网络规模也变为了大型甚至可以说是超大型网络,这这个背景下,如何计算一个网络是否平衡便成为该领域的主要热点问题。
(1) Heider理论(强平衡理论SBT)。
(2) 结构平衡理论(Structural Balance Theroem):在完全符号网络中,网络平衡的充要条件是其所有的三元组(回路)都平衡。
结构平衡的推论:一个完全符号网络平衡的充要条件是它可以被分为两部分X和Y,X和Y内部的节点连接均为正连接,X和Y之间的连接均为负连接。
(3) 弱平衡理论(A weaker form of structural balance,WSBT):如果完全符号网络中不存在这样的三元组:两个边为正,一边为负,则该网络称为是弱平衡网络。
对于弱平衡理论而言,上图的三元组中,三边均为负连接的三元组也属于平衡三元组,也就是三元组的四种情况有三种属于平衡状态,一个属于不平衡状态(两边为正,一边为负)。
弱平衡网络推论:如果一个网络为弱平衡理论,那么它可以分为多个部分,每部分内的连接为正,部分之间的连接为负。
(4) 对任意网络平衡的定义.
1) 对于一个任意网络而言,如果我们可以将它所缺失的边填充使它成为一个平衡的完全符号网络,那么原网络就是平衡网络;
2) 对于一个任意网络而言,如果我们可以将它分为两部分,使得每个部分内的连接均为实线,部分之间的连接均为虚线。
以上的两种定义是等价的。
一个符号网络平衡的充要条件是它不包括含有奇数个负连接的回路。
(5) 近似平衡网络(略)。
3.3 网络平衡的计算(A spectral algorithm for computing social balance)
命题1:节点i参与的三元组数目
A为邻接矩阵,元素取值可能为:1,-1,0;
G为邻接矩阵,元素取值可能为:0,1.
命题2:对于节点i而言,bi为其参与的平衡三元组数目,ui为其参与的不平衡三元组数目,则
理论1:对于完全符号图而言,
平衡三元组所占的比例为
理论2:对于任意符号网络,平衡三元组所占的比例为
注:以上两个计算网络平衡的公式中,特征值可以随大到小选择前几个比较大的,就像PCA那样,这样可以使得计算的复杂度大大减小。
随着各种在线社交平台的发展,社交平台(比如QQ、微博、朋友圈等)已经不仅仅是一种用户进行沟通的社交平台,它们更是社会信息产生和传播的一种主要的媒介。影响最大化(Influence Maximization)同结构平衡一样,也是针对社会网络的研究而被提出的,它来源于经济学的市场营销。2001年,影响最大化被Domins首次以一种算法问题的形式被提出。而影响最大化受到广泛的关注是在2003年Kempe等人在当年的KDD会议上发表的一篇有关影响最大化的论文之后,随后各种影响最大化算法被迅速提出,最近的十几年里,影响最大化的相关文章达到了上千篇,可见这个问题还是很值得关注的。
影响最大化问题可以这样来描述:一个商家或者企业利用一种社交平台(比如为新浪微博)为自己的新产品或者新服务进行推广,如何在资金有限的情况下雇佣微博达人来做推广可以使得推广范围达到最大?
我们再给出影响最大化的一般定义:
给定一个网络[Math Processing Error]和一个整数[Math Processing Error](一般小于50),如何在[Math Processing Error]中找出[Math Processing Error]个节点,使得这[Math Processing Error]的节点组成的节点集合[Math Processing Error]的影响传播范围[Math Processing Error]达到最大。
根据上述影响最大化的定义我们很容易可以知道,影响最大化本身属于一种组合优化问题。常用的影响最大化传播模型有独立级联传播模型(ICM)和线性阈值传播模型(LTM)。
影响最大化方面的主要算法可以分为如下几类:
(1)基于网络中心性的启发式方法:比如最大度方法、最短平均距离方法、PageRank方法等;
(2)基于子模块性的贪婪方法:比如最经典的Greedy算法,CELF算法以及后来的NewGreedy和CELF++等;
(3)基于社区结构的方法:比如CGA算法、CIM算法等;
(4)基于目标函数优化的方法:比如模拟退火算法等。
网络传播领域涉及很多方面,比如网络节点重要性排序、网络鲁棒性分析、网络信息爆发阈值优化等。这些领域都很有意思,感兴趣的博友可以好好深入研究一下。
首先在这里推荐两款我常用的网络可视化工具:Pajek (点击进入官方网站)、Gephi(点击进入官方网站)。
下边为pajek可视化窗口下的一个网络拓扑结构图:

这是Gephi的一个可视化效果:
常用的一些公开数据集整理:
Pajek(可视化工具)数据集:http://vladowiki.fmf.uni-lj.si/doku.php?id=pajek:data:index;
Newman(复杂网络科学领域大牛)个人数据集:http://www-personal.umich.edu/~mejn/netdata/
Stanford大学大规模网络数据集:http://snap.stanford.edu/data/
复旦大学网络数据集整理:http://gdm.fudan.edu.cn/GDMWiki/Wiki.jsp?page=Network%20DataSet
KONECT数据集整理:http://konect.uni-koblenz.de/
[1] Grivan and Newman. Community structure in social and biological networks. PNAS, 2002.
[2] Newman and Grivan. Finding and evaluating community structure in networks. PRE, 2004.
[3] Newman. Networks: an introduction. 2010.
[4] Cartwright and Harary. Structural balance: a generalization of Heider‘s theory. 1956.
[5] Facchetti et al. Computing global structural balance in large-scale signed social networks. 2011.
[6] Kempe et al. Maximizing the spread of influence through a social network. 2003.
[7] Chen et al. Efficient influence maximization in social networks. 2009.
[8] 任晓龙,吕琳媛. 网络重要节点排序方法综述. 2014.
标签:
原文地址:http://www.cnblogs.com/DjangoBlog/p/5257498.html