标签:
矩阵快速幂。
样例是这样构造矩阵的:
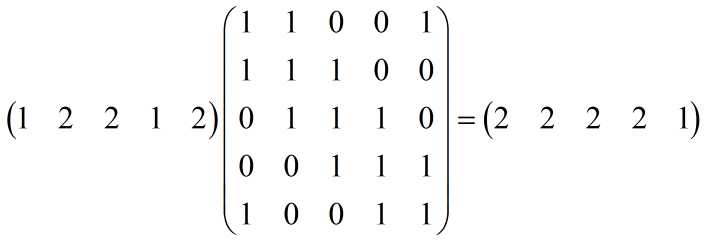
矩阵很好构造,但是500*500*500*logk的复杂度显然是无法通过这题的。
其实本题构造出来的矩阵是一个循环矩阵,只需直到第一行或者第一列,即可直到整个矩阵是怎么样的。
所以,中间计算的时候,需要直到第一行是什么即可,即1*n的矩阵乘n*n的矩阵。时间复杂度o(n*n*logk)
#include<cstdio> #include<cstring> #include<cmath> #include<vector> #include<algorithm> using namespace std; const int maxn=500+10; int n,d,k; long long mod; long long z[maxn],a[maxn]; long long y[maxn],x[maxn]; long long tmp[maxn][maxn]; long long r[maxn]; void init() { memset(y,0,sizeof y); y[1]=1; memset(x,0,sizeof x); x[1]=1; for(int i=2; i<=1+d; i++) x[i]=1; for(int i=n; i>=n-d+1; i--)x[i]=1; } int main() { while(~scanf("%d%lld%d%d",&n,&mod,&d,&k)) { for(int i=1; i<=n; i++) scanf("%lld",&z[i]); init(); while(k) { for(int i=1; i<=n; i++) { int tot=1; for(int j=i; j<=n; j++) tmp[i][j]=x[tot++]; for(int j=1; j<=i-1; j++) tmp[i][j]=x[tot++]; } if(k%2==1) { for(int j=1; j<=n; j++) { long long sum=0; for(int t=1; t<=n; t++) sum=(sum+(y[t]*tmp[j][t])%mod)%mod; r[j]=sum; } for(int j=1; j<=n; j++) y[j]=r[j]; k--; } else if(k%2==0) { for(int j=1; j<=n; j++) { long long sum=0; for(int t=1; t<=n; t++) sum=(sum+(x[t]*tmp[j][t])%mod)%mod; r[j]=sum; } for(int j=1; j<=n; j++) x[j]=r[j]; k=k/2; } } for(int i=1; i<=n; i++) { int tot=1; for(int j=i; j<=n; j++) tmp[i][j]=y[tot++]; for(int j=1; j<=i-1; j++) tmp[i][j]=y[tot++]; } for(int j=1; j<=n; j++) { long long sum=0; for(int t=1; t<=n; t++) sum=(sum+(z[t]*tmp[j][t])%mod)%mod; r[j]=sum; } for(int j=1; j<=n; j++) { printf("%d",r[j]); if(j<n) printf(" "); else printf("\n"); } } return 0; }
标签:
原文地址:http://www.cnblogs.com/zufezzt/p/5258210.html