标签:
?
1021?石子归并?V1 N堆石子摆成一条线。现要将石子有次序地合并成一堆。规定每次只能选相邻的2堆石子合并成新的一堆,并将新的一堆石子数记为该次合并的代价。计算将N堆石子合并成一堆的最小代价。 ? 例如: 1 2 3 4,有不少合并方法 1 2 3 4 => 3 3 4(3) => 6 4(9) => 10(19) 1 2 3 4 => 1 5 4(5) => 1 9(14) => 10(24) 1 2 3 4 => 1 2 7(7) => 3 7(10) => 10(20) ? 括号里面为总代价可以看出,第一种方法的代价最低,现在给出n堆石子的数量,计算最小合并代价。 Input 第1行:N(2 <= N <= 100) 第2 - N + 1:N堆石子的数量(1 <= A[i] <= 10000) Output 输出最小合并代价 Input示例 4 1 2 3 4 Output示例 19 |
?
?
1022?石子归并?V2 N堆石子摆成一个环。现要将石子有次序地合并成一堆。规定每次只能选相邻的2堆石子合并成新的一堆,并将新的一堆石子数记为该次合并的代价。计算将N堆石子合并成一堆的最小代价。 ? 例如: 1 2 3 4,有不少合并方法 1 2 3 4 => 3 3 4(3) => 6 4(9) => 10(19) 1 2 3 4 => 1 5 4(5) => 1 9(14) => 10(24) 1 2 3 4 => 1 2 7(7) => 3 7(10) => 10(20) ? 括号里面为总代价可以看出,第一种方法的代价最低,现在给出n堆石子的数量,计算最小合并代价。 Input 第1行:N(2?<=?N?<=?1000) 第2?-?N?+?1:N堆石子的数量(1?<=?A[i]?<=?10000) Output 输出最小合并代价 Input示例 4 1 2 3 4 Output示例 19 |
?
第一题比较好写,复杂度是n3,但是第二题就需要用到四边形不等式优化,把复杂度降为n2。
《算法竞赛入门经典训练指南-刘汝佳》P170(老版)
书中在讨论最优排序二叉树时提到四边形不等式优化方法。一般地,对于类似的状态转移方程:
????d[i,j] = max{ d[i,k?1] + d[k+1,j] } + w[i,j]
状态有O(n2 )个,每个决策有O(n),因此时间复杂度为O(n3)。
下面把它优化到O(n2)。
四边形不等式(Monge condition / Quadrangle inequality) 如果对于i ≤ i‘ < j ≤ j‘ 总有w[i,j] + w[i‘ ,j‘ ] ≤ w[i‘ ,j] + w[i ,j‘],称w满足四边形不等式,或w满足凸性。
区间包含格上的单调性 如果对于i ≤ i‘ < j ≤ j‘ 总有w[i‘ ,j] ≤ w[ i , j‘ ],称w满足单调性,也就是说对于两个区间q1,q2(q2包含q1),w[q1] ≤ w[q2]。
定理(F.Yao):若w满足四边形不等式,则d也满足四边形不等式,即
d[i,j] + d[i‘ ,j‘ ] ≤ d[ i‘ ,j] + d[ i ,j‘ ] , i ≤ i‘ ≤ j ≤ j‘
证明略。
更进一步地,d的凸性可以推出决策单调性。记k[i,j]为让d[i,j]取最小值的决策,有
定理(F.Yao):k[i,j] ≤ k[i,j + 1] ≤ k[i + 1,j + 1], i ≤ j,即k在同行同列都是递增的。
证明:由对称性,只需证明k[i,j] ≤ k[i,j + 1]。记dk[i,j] = d[i,k ? 1] + d[k,j] +w[i,j],则只需证明对所有的i < k ≤ k‘ ≤ j,如果dk‘[i,j] ≤ dk [i,j],那么dk‘ [i,j + 1] ≤dk [i,j + 1],即:区间加长一个单位后,以前较好的决策现在仍然好。事实上,可以证明一个更强的结论:dk [i,j]?d k‘[i,j] ≤ d k [i,j +1]?dk‘ [i,j +1](i <k ≤ k‘ ≤ j),因为当k‘在[i,j]更优时,左边≥0,由不等式知右边≥0,因此k‘仍更优。
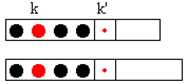
如上图,设k‘ 是[i,j]的最优值,则对于它左边的任意k,k‘ 在[i,j]上更优意味着k‘ 在[i,j+1]上仍最优,因此k‘ 左边的任意k在[i,j+1]上仍然不是最大值,即k[i,j + 1] ≥ k[i,j]。
欲证dk [i,j] – dk‘ [i,j] ≤ dk [i,j + 1] – dk‘ [i,j + 1](i < k ≤ k‘ ≤ j),
移项得:dk [i,j] +dk‘ [i,j + 1] ≤ dk [i,j + 1] + dk‘ [i,j]。
按定义展开,两边消去w[i,j] + w[i,j + 1] + d[i,k ?1] + d[i,k 0 ? 1]得:
????????d[k,j] + d[k‘ ,j + 1] ≤ d[k,j + 1] + d[k‘ ,j]
这就是d的凸性。
有了决策单调性,可以稍微改造一下程序,决策从k[i,j?1]枚举到k[i+1,j]即可。
这样做时间复杂度降低了吗?当L = j ? 1固定时,
d[1,L + 1]的决策是k[1,L] ~ k[2,L + 1]
d[2,L + 2]的决策是k[2,L + 1] ~ k[3,L + 2]
d[3,L + 3]的决策是k[3,L + 2] ~ k[4,L + 3]
d[4,L + 4]的决策是k[4,L + 3] ~ k[5,L + 4]
...
合并起来,当L固定时总决策为k[1,L] ~ k[n?L+1,n],共O(n)个。由于L有O(n),因此总时间复杂度降为O(n 2 )。
?
以上所给出的状态转移方程只是一种比较一般的,其实,很多状态转移方程都满足四边形不等式优化的条件。
解决这类问题的大概步骤是:
?
不管m[i,j]=opt{m[i,k]+m[k,j]+w[i,j]}的opt是min还是max,每一步的决策从k[i,j?1]枚举到k[i+1,j]即可。这样就能降低复杂度了。就51nod这道题来说,它的步骤也是如此。
标签:
原文地址:http://www.cnblogs.com/lastone/p/5263072.html