标签:http os 2014 for re c 问题 ar
最小二乘法的直线拟合
#coding:utf-8 import numpy as np import matplotlib.pyplot as plt dots = np.array([[1,6], [2,5], [3,7], [4,10]]) plt.plot([i[0] for i in dots], [i[1] for i in dots], ‘ro‘) plt.axis([0, 6, 0, 12]) def nihezhixian(k, x, b): return k*x + b sumxy = sum([a[0]*a[1] for a in dots]) #print sumxy sumxx = sum([a[0] ** 2 for a in dots]) print sumxx sumx = sum([a[0] for a in dots]) print sumx sumy = sum([a[1] for a in dots]) #a0 = (∑Yi) / n - a1(∑Xi) / n (式1-8) #a1 = [n∑Xi Yi - (∑Xi ∑Yi)] / [n∑Xi2 - (∑Xi)2 )] (式1-9) # print dir(dots) n = dots.shape[0] k = float(n*sumxy - sumx*sumy)/float(n*sumxx - sumx*sumx) # print a1 b = float(sumy)/n - float(k * sumx) / n plt.plot([i[0] for i in dots], [nihezhixian(k, i[0], b) for i in dots]) plt.show()
图像输出如下
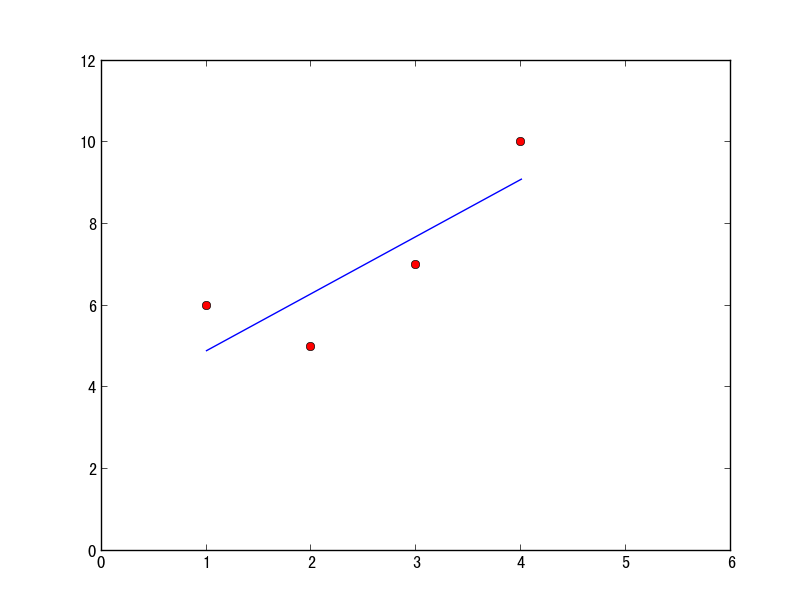
最小二乘法,实际上解决的问题是:对于给定的一系列点[(x1,y1), (x2,y2)...(xn,yn)],来的到y关于x的函数。
求一个函数y=f(x),使得y=f(x)能够描述这一些列点也就是解决如下方程:
Sum(f(xi) - yi)**2
有最小值,在直线的拟合过程中,y = f(x) = ax + b。带入上面式子,这是一个求最小值的问题,那么只需要对a,b求偏倒数即可.
标签:http os 2014 for re c 问题 ar
原文地址:http://my.oschina.net/fsxchen/blog/294857