标签:
首先写写本周的仿真作业。仿真结果:启动后约在3.9至4.2秒转速会达到稳定,稳定值在1213r/min左右(不能达到1220r/min,因为一直会有0.6欧姆的内阻存在),而上升曲线只有些许波澜。
仿真要求:电机启动仿真要求结合要本周学习的直流电机机械特性,用Modelica设计和仿真一个直流电机串电阻启动过程,电机工作在额定电压和额定磁通下,采用串三段或四段电阻启动,整个启动过程电枢电流中不能超过额定电流的3倍。额定电压240V,额定电流16.2A,额转矩29.2N.m,额定转速1220 r/min,转动惯量1 Kg.m^2,电枢电阻0.6 Ohm,转矩常数(额定磁通)1.8,电动势常数(额定磁通)0.189,
仿真过程:
由于转速n不能突变,这说明反电动势E也不能突变,于是在切换电阻的时候电阻两端的电压事实上是没有变化的,于是变化前后的电压满足I1*R1=I2*R2,当把这个公式推广到m级启动时
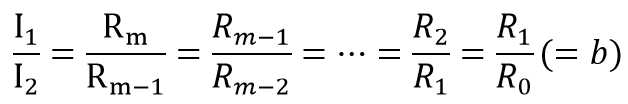
其中b为比例系数,对于本次的仿真我采用四段串阻启动,并让每次换电阻值之后的电流值I1尽量接近极限值即48.6A,因为较大的电流表明会有较大的转矩,转速n的变化速度也会更快,从而能够更快地到达稳定转速缩短启动时间。为了尽量提升I1的值我将I2的值设为较高的b*I2,于是可以算出:
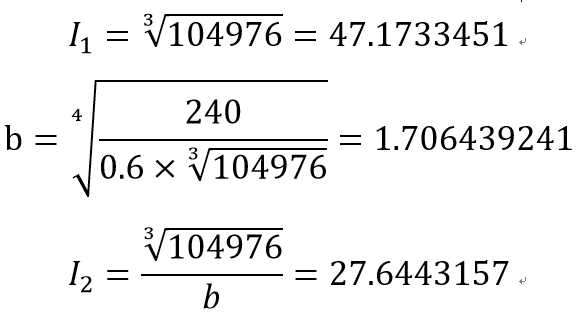
依次可以算出电阻的值(单位欧姆)按时间顺序为5.087618856, 2.98142397, 1.747160929, 1.023863544, 0.6。所以按照仿真的模型来看,R_ad的值为4.487618856, 2.38142397, 1.147160929, 0.423863544, 0。
所以只需要通过程序找到应该改变电阻值的时间点,即电流每一次从I1下降到I2时的时间点,并在那时改变电阻值就可以了。
Modelica里面时间分为两种,即状态事件和时间事件,所以我们可以通过程序让电流值达到我们的要求状态时触发电阻值的变化,此时需要又modelica帮我们算出事件发生的时间点,也可以自行算出事件发生的时间点,然后用时间事件的形式写程序。
由于多次尝试没有成功写出利用状态事件可以仿真的模型,所以最后是使用modelica一次一次尝试不同电阻值并从仿真结果中读取大致时间值而写出的只有时间事件的模型。首先附上一直报错的模型,希望老师能够帮忙看下里面有什么问题:
model motor "An DC Motor Model"
type Voltage=Real(unit="V");
type Current=Real(unit="A");
type Resistance=Real(unit="Ohm");
type Speed=Real(unit="r/min");
type Torque=Real(unit="N.m");
type Inertia=Real(unit="kg.m^2");
Torque Tm"Torque of the Motor";
Speed n"Speed of the Motor";
Current i"Armature Current";
Voltage u"Voltage Source";
Resistance R_ad"External Resistance";
Real c = 0;
parameter Real J = 1"Total Inertia";
parameter Real R = 0.6"Armature Resistance";
parameter Real Kt = 1.8"Torque Constant";
parameter Real Ke = 0.189"EMF Constant";
parameter Real Tl = 29.2"Load Torque";
parameter Real b=1.706439241;
initial equation
R_ad=5.087618856;
equation
Tm-Tl = J * der(n) * 6.28 / 60;
Tm= Kt * i;
u= i * R_ad + Ke * n;
if time <= 0.1 then
u =0;
else
u =240;
end if;
if time>0.2 and i<27.7 and pre(R_ad)>5 then R_ad=2.98142397;
elseif time>0.2 and i<27.7 and pre(R_ad)>2 then R_ad=1.747160929;
elseif time>0.2 and i<27.7 and pre(R_ad)>1.5 then R_ad=1.023863544;
elseif time>0.2 and i<27.7 then R_ad=0.6;
else R_ad=pre(R_ad);
end if;
end motor;
然后附上最后多次试验得到的结果图以及代码。可以看出该电机4秒趋于平稳,曲线波动也不大。
正确的模型如下:
model motor1 "An DC Motor Model"
type Voltage=Real(unit="V");
type Current=Real(unit="A");
type Resistance=Real(unit="Ohm");
type Speed=Real(unit="r/min");
type Torque=Real(unit="N.m");
type Inertia=Real(unit="kg.m^2");
Torque Tm"Torque of the Motor";
Speed n"Speed of the Motor";
Current i"Armature Current";
Voltage u"Voltage Source";
Resistance R_ad"External Resistance";
parameter Real J = 1"Total Inertia";
parameter Real R = 0.6"Armature Resistance";
parameter Real Kt = 1.8"Torque Constant";
parameter Real Ke = 0.189"EMF Constant";
parameter Real Tl = 29.2"Load Torque";
equation
Tm-Tl = J * der(n) * 6.28 / 60;
Tm= Kt * i;
u= i * (R+R_ad) + Ke * n;
if time <= 0.1 then u = 0;
else
u = 240;
end if;
if time <= 1.7 then
R_ad = 4.487618856;
elseif time <=2.6 then
R_ad = 2.38142397;
elseif time <=3.14 then
R_ad = 1.147160929;
elseif time <=3.455 then
R_ad = 0.423863544;
else
R_ad = 0;
end if;
end motor1;
图像如下:(首先是电流的图像然后是转速的图像)
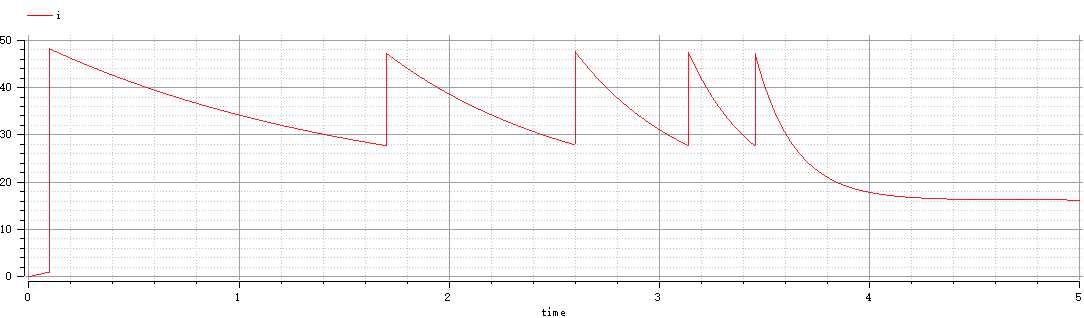
电流图
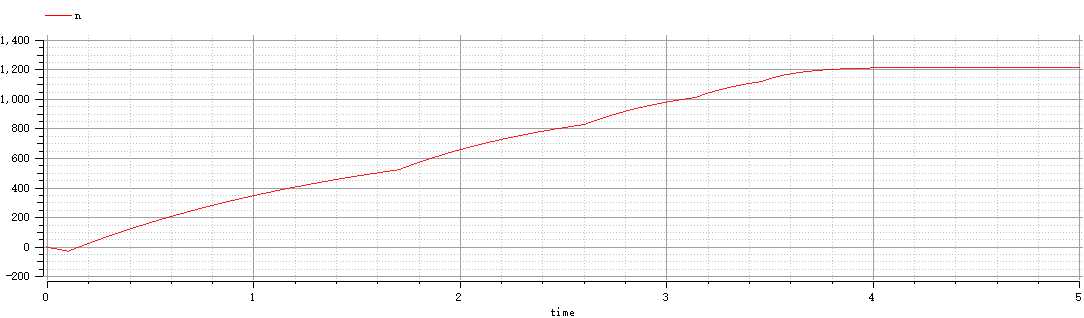
转速图
学习笔记:
书本上第四章里面的主角时三相异步电动机,出于兴趣其工作原理在高二的时候就已经和物理老师有过一些交流,所以并不陌生,然而其工作原理里面好多公式和细节必然是当时所不知,粗略看过之后觉得易忽视的地方是单相的电流和多相电流的混合值之间的关系。而图像自然也是分析其机械特性的不可少工具。可以类比直流电机来学习。
特斯拉的故事感觉像是非常神话一般,极其异于常人的感觉有些难以置信,但他出色的发明能力和对交流电以及电流世界给他创造出来的绮丽视界让他入迷程度描写得都是非常真实的。电流之战中我看到了一个和想象中大不一样的爱迪生。但爱迪生对直流电的固执其实和所有其他读书人一样,坚持认为自己是对的自然会有强烈的排外感产生,但是使用的略显卑鄙的商业手段和舆论宣传还是让我胆寒。在电动机历史里面交流电替换直流电似乎是历史上理所当然的一笔,这段时期的事情一句话就被带过去了,但是其间的事件错综复杂,人类历史上这么大的进步确实是不容易。而特斯拉也找到了难得的友情,度过了这一风雨。金钱俨然已经不重要了。科学家发明家们在科学的推进中的支持和反对确实不是一个证明题的对错的问题,这其中牵扯的还有种种利害关系,但是归于本心,立足科学本身才是正确的选择。
标签:
原文地址:http://www.cnblogs.com/quartet/p/5264022.html