标签:
图的遍历
广度优先遍历类似于树的按层次遍历,具体过程如下:
(1)从数组中选择一个未被访问的顶点Vi,将其标记为已访问。
(2)接着依次访问Vi的所有未被访问的邻接点,并标记为已被访问过。
(3)从这些邻接点出发进行广度优先遍历,直至图中所有和Vi有路径相通的顶点都被访问过。
(4)重复步骤(1)至步骤(3)的操作,直至所有顶点都被访问过。
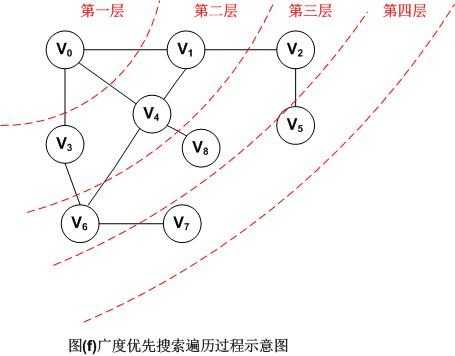
图(f)采用广度优先搜索遍历以V0为出发点的顶点序列为:V0,V1,V3,V4,V2,V6,V8,V5,V7
深度优先遍历方法类似于树的先序遍历,具体过程如下:
(1)从数组中选择一个未被访的顶点Vi,将其标记为已访问。
(2)接着从Vi的一个未被访问过的邻接点出发进行深度优先遍历。
(3)重复步骤(2),直至图中所有和Vi有路径相通的顶点都被访问过。
(4)重复步骤(1)至步骤(3)的操作,直至所有顶点都被访问过。
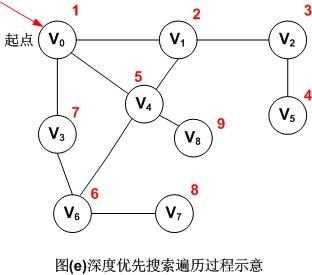
红色数字代表遍历的先后顺序,所以图(e)无向图的深度优先遍历的顶点访问序列为:V0,V1,V2,V5,V4,V6,V3,V7,V8
程序编写<GraphTrav>:
#include <stdio.h> #include "AdjMatrixGraph.c"//之前邻接矩阵保存图法时编写的 #define QUEUE_MAXSIZE 30 //队列的最大容量 typedef struct { int Data[QUEUE_MAXSIZE]; //数据域 int head; //队头指针 int tail; //队尾指针 }SeqQueue; //队列结构 //队列操作函数 void QueueInit(SeqQueue *q); //初始化一个队列 int QueueIsEmpty(SeqQueue q); //判断队列是否空 int QueueIn(SeqQueue *q,int n); //将一个元素入队列 int QueueOut(SeqQueue *q,int *ch); //将一个元素出队列 //图操作函数 void DFSTraverse(MatrixGraph *G); //深度优先遍历 void BFSTraverse(MatrixGraph *G); //广度优先遍历 void DFSM(MatrixGraph *G,int i); void BFSM(MatrixGraph *G,int i); void QueueInit(SeqQueue *Q) //队列初始化 { Q->head=Q->tail=0; } int QueueIsEmpty(SeqQueue Q) //判断队列是否已空,若空返回1,否则返回0 { return Q.head==Q.tail; } int QueueIn(SeqQueue *Q,int ch) //入队列,成功返回1,失败返回0 { if((Q->tail+1) % QUEUE_MAXSIZE ==Q->head) //若队列已满 return 0; //返回错误; Q->Data[Q->tail]=ch; //将数据ch入队列 Q->tail=(Q->tail+1) % QUEUE_MAXSIZE; //调整队尾指针 return 1; //成功,返回1 } int QueueOut(SeqQueue *Q,int *ch) //出队列,成功返回1,并用ch返回该元素值,失败返回0 { if(Q->head==Q->tail) //若队列为空 return 0; //返回错误 *ch=Q->Data[Q->head]; //返回队首元素 Q->head=(Q->head+1) % QUEUE_MAXSIZE; //调整队首指针 return 1; //成功出队列,返回1 } void DFSTraverse(MatrixGraph *G) //深度优先遍历 { int i; for(i=0;i<G->VertexNum;i++) //清除各顶点遍历标志 G->isTrav[i]=0; printf("深度优先遍历结点:"); for(i=0;i<G->VertexNum;i++) if(!G->isTrav[i]) //若该点未遍历 DFSM(G,i); //调用函数遍历 printf("\n"); } void DFSM(MatrixGraph *G,int i) //从第i个结点开始,深度遍历图 { int j; G->isTrav[i]=1; //标记该顶点已处理过 printf("->%c",G->Vertex[i]);//输出结点数据 // printf("%d->",i); //输出结点序号 //添加处理节点的操作 for(j=0;j<G->VertexNum;j++) if(G->Edges[i][j]!=MAXVALUE && !G->isTrav[i]) DFSM(G,j); //递归进行遍历 } void BFSTraverse(MatrixGraph *G) //广度优先 { int i; for (i=0;i<G->VertexNum;i++) //清除各顶点遍历标志 G->isTrav[i]=0; printf("广度优先遍历结点:"); for (i=0;i<G->VertexNum;i++) if (!G->isTrav[i]) BFSM(G,i); printf("\n"); } void BFSM(MatrixGraph *G,int k) //广度优先遍历 { int i,j; SeqQueue Q; //创建循环队列 QueueInit(&Q); //初始化循环队列 G->isTrav[k]=1; //标记该顶点 printf("->%c",G->Vertex[k]); //输出第一个顶点 //添加处理节点的操作 QueueIn(&Q,k); //入队列 while (!QueueIsEmpty(Q)) //队列不为空 { QueueOut(&Q,&i); //出队列 for (j=0;j<G->VertexNum;j++) if(G->Edges[i][j]!=MAXVALUE && !G->isTrav[j]) { printf("->%c",G->Vertex[j]); G->isTrav[j]=1; //标记该顶点 //处理顶点 QueueIn(&Q,j); //出队列 } } }
事件:
#include <stdio.h> #include "GraphTrav.c" int main() { MatrixGraph G; //定义保存邻接表结构的图 int path[VERTEX_MAX]; int i,j,s,t; char select; do { printf("输入生成图的类型(0:无向图,1:有向图):"); scanf("%d",&G.GraphType); //图的种类 printf("输入图的顶点数量和边数量:"); scanf("%d,%d",&G.VertexNum,&G.EdgeNum); //输入图顶点数和边数 for(i=0;i<G.VertexNum;i++) //清空矩阵 for(j=0;j<G.VertexNum;j++) G.Edges[i][j]=MAXVALUE; //设置矩阵中各元素的值为0 CreateMatrixGraph(&G); //生成邻接表结构的图 printf("邻接矩阵数据如下:\n"); OutMatrix(&G); //输出邻接矩阵 DFSTraverse(&G); //深度优先搜索遍历图 BFSTraverse(&G); //广度优先搜索遍历图 printf("图遍历完毕,继续进行吗?(Y/N)"); scanf(" %c",&select); }while(select!=‘N‘ && select!=‘n‘); getch(); return 0; }
结果:
标签:
原文地址:http://www.cnblogs.com/moguwang/p/5287617.html