标签：
动态规划概述
动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题逐个求解，创立了解决这类过程优化问题的新方法——动态规划。
动态规划算法基本思想
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。
动态规划算法基本结构
(1)确定问题的决策对象。
(2)对决策过程划分阶段。
(3)对各阶段确定状态变量。
(4)根据状态变量确定费用函数和目标函数。
(5)建立各阶段状态变量的转移过程，确定状态转移方程。
动态规划的基本定理和基本方程
对于初始状态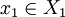
，策略
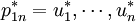是最优策略的充要条件是对于任意的k,
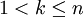,有
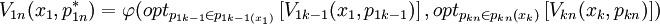
若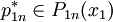
是最优策略，则对于任意的k,1<k<n，它的子策略
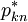对于由x1和
确定的以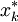
为起点的第k到n后部子过程而言，也是最优策略。
上述推论称为最优化原理，它给出了最优策略的必要条件，通常略述为：不论过去的状态和决策如何，对于前面的决策形成的当前的状态而言，余下的各个决策必定构成最优策略。
根据基本定理的推论可以得到动态规划的基本方程：
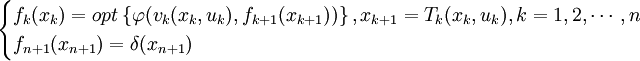(1)
其中fn + 1(xn + 1) = δ(xn + 1)是决策过程的终端条件，δ为一个已知函数。当xn + 1只取固定的状态时称固定终端；当xn + 1可在终端集合Xn + 1中变动时称自由终端。最终要求的最优指标函数满足(2)式：
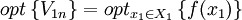(2)
(1)式是一个递归公式，如果目标状态确定，当然可以直接利用该公式递归求出最优值（这种递归方法将在后文介绍，称作备忘录法），但是一般在实际应用中我们通常将该递归公式改为递推公式求解，这样一般效率会更高一些。
标签：
原文地址：http://www.cnblogs.com/wqkant/p/5290096.html
