标签:
由于不是计算机专业的学生,很遗憾我们专业并没有开数据结构这门课。现在学习数据结构的网课,也购买了教材;教材上给了大部分的代码,但是我还是打算根据网课和课本整理一遍,自己打一遍代码,去调试通过。呐、希望自己不会半途而废 (^-^)V
一.关于空间的使用
Eg:写程序实现一个函数PrintN,使得传入一个正整数N的参数,能顺序打印从1到N的全部正整数。
1 //循环实现 2 void PrintN1 (int N) 3 { 4 for (int i = 1; i <= N; i++) { 5 printf("%d\n", i); 6 } 7 } 8 //递归实现 9 void PrintN2 (int N) 10 { 11 if(N) { 12 PrintN2(N - 1); 13 printf("%d\n", N); 14 } 15 }
结果:当测试数N较大时,例如100,000,用循环可以得出结果,而用递归函数则程序停止运行退出。
递归算法其优点为是代码简洁清楚,易理解;缺点在于对空间的占用大。
由此例可见,解决问题方法的效率跟空间的利用效率有关。
二.关于算法效率
学习计时函数:clock():捕捉从程序开始运行到clock()被调用时所耗费的时间。这个时间单位是clock tick。其头文件为time.h。
常数CLK_TCK:机器始终每秒所走的clock tick数。
1 #include <stdio.h> 2 #include <time.h> 3 clock_t start, stop; //clock_t是clock()函数返回的变量类型 4 double duration; //记录被测函数运行时间,以秒为单位 5 int main() 6 { 7 //不在测试范围内的准备工作写在clock()调用之前 8 start = clock(); //开始计时 此时clock()返回从主函数开始到clock()被调用的时间 9 MyFunction(); //此处加需测试函数 10 stop = clock(); //停止计时 此时clock()返回从主函数开始到此clock()被调用的时间 11 duration = ((double)(stop - start)) / CLK_TCK; 12 //其他不在测试范围的处理写在后面,例如输出duration的值 13 return 0; 14 }
Eg:写程序计算给定多项式 ![]() 在给定点x=1.1处的值f(1.1)。
在给定点x=1.1处的值f(1.1)。
方法一:各项展开得![]() 易得
易得
1 double f1(int n, double a[], double x) { 2 double sum = a[0]; 3 for(int i = 1; i <= n; i++) 4 sum += (a[i] * pow(x,i)); 5 return sum; 6 }
数组a[]存放了x前的系数,n为控制最高项系数。pow(x,y) 为计算x的y次幂,在vc6中定义为double pow(double x, double y)头文件math.h。此处n=9, a[i] = i。
方法二:![]()
1 double f2(int n, double a[], double x) { 2 double sum = a[n]; 3 for(int i = n; i > 0; i--) 4 sum = a[i-1] + x*sum; 5 return sum; 6 }
少了调用pow()函数,重复多次x自乘,增加了效率。
用clock()验证,由于一次运行所用时间短于一个clock tick,所以我们重复多次测量。

1 #include <stdio.h> 2 #include <time.h> 3 #include <math.h> 4 #define MaxN 10 //最高次数 5 #define Max_count 1e7 //函数被调用的最大次数 6 7 double f1(int n, double a[], double x); 8 double f2(int n, double a[], double x); 9 10 int main() 11 { 12 clock_t start, stop; //clock_t是clock()函数返回的变量类型 13 double duration; //记录被测函数运行时间,以秒为单位 14 //不在测试范围内的准备工作写在clock()调用之前 15 double a[MaxN]; 16 for(int i = 0; i < MaxN; i++) //写入系数,存于a[] 17 a[i] = i; 18 start = clock(); //开始计时 此时clock()返回从main函数开始到clock()被调用的时间 19 for(int i = 0; i < Max_count; i++) 20 f1(9, a, 1.1); //此处加需测试函数 测试函数1 21 stop = clock(); //停止计时 此时clock()返回从main函数开始到此clock()被调用的时间 22 duration = ((double)(stop - start)) / CLK_TCK / Max_count; 23 //其他不在测试范围的处理写在后面,例如输出duration的值 24 printf("方法一 所用clock tick: %f\n", (double)(stop - start)); 25 printf("方法一 所用时间(s): %f\n", duration); 26 27 start = clock(); //开始计时 此时clock()返回从main函数开始到clock()被调用的时间 28 for(int i = 0; i < Max_count; i++) 29 f2(9, a, 1.1); //此处加需测试函数 测试函数1 30 stop = clock(); //停止计时 此时clock()返回从main函数开始到此clock()被调用的时间 31 duration = ((double)(stop - start)) / CLK_TCK / Max_count; 32 //其他不在测试范围的处理写在后面,例如输出duration的值 33 printf("方法二 所用clock tick: %fd\n", (double)(stop - start)); 34 printf("方法二 所用时间(s): %f\n", duration); 35 return 0; 36 } 37 //方法一 38 double f1(int n, double a[], double x) { 39 double sum = a[0]; 40 for(int i = 1; i <= n; i++) 41 sum += (a[i] * pow(x,i)); 42 return sum; 43 } 44 //方法二 45 double f2(int n, double a[], double x) { 46 double sum = a[n]; 47 for(int i = n; i > 0; i--) 48 sum = a[i-1] + x*sum; 49 return sum; 50 }
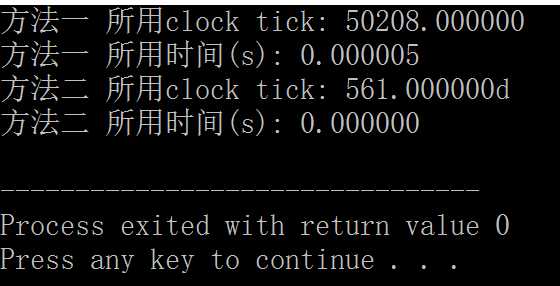
方法一和方法二时间相差的是数量级!
由此例可见,解决问题方法的效率跟算法的巧妙程度有关。

同理。

1 #include <stdio.h> 2 #include <time.h> 3 #include <math.h> 4 #define MaxN 101 //最高次数 5 #define Max_count 1e7 //函数被调用的最大次数 6 7 double f1(int n, double a[], double x); 8 double f2(int n, double a[], double x); 9 10 int main() 11 { 12 clock_t start, stop; //clock_t是clock()函数返回的变量类型 13 double duration; //记录被测函数运行时间,以秒为单位 14 //不在测试范围内的准备工作写在clock()调用之前 15 double a[MaxN]; 16 a[0] = 1.0; 17 for(int i = 1; i < MaxN; i++) //写入系数,存于a[] 18 a[i] = 1.0 / i; 19 start = clock(); //开始计时 此时clock()返回从main函数开始到clock()被调用的时间 20 for(int i = 0; i < Max_count; i++) 21 f1(100, a, 1.1); //此处加需测试函数 测试函数1 22 stop = clock(); //停止计时 此时clock()返回从main函数开始到此clock()被调用的时间 23 duration = ((double)(stop - start)) / CLK_TCK / Max_count; 24 //其他不在测试范围的处理写在后面,例如输出duration的值 25 printf("方法一 所用clock tick: %f\n", (double)(stop - start)); 26 printf("方法一 所用时间(s): %f\n", duration); 27 28 start = clock(); //开始计时 此时clock()返回从main函数开始到clock()被调用的时间 29 for(int i = 0; i < Max_count; i++) 30 f2(100, a, 1.1); //此处加需测试函数 测试函数1 31 stop = clock(); //停止计时 此时clock()返回从main函数开始到此clock()被调用的时间 32 duration = ((double)(stop - start)) / CLK_TCK / Max_count; 33 //其他不在测试范围的处理写在后面,例如输出duration的值 34 printf("方法二 所用clock tick: %fd\n", (double)(stop - start)); 35 printf("方法二 所用时间(s): %f\n", duration); 36 return 0; 37 } 38 //方法一 39 double f1(int n, double a[], double x) { 40 double sum = a[0]; 41 for(int i = 1; i <= n; i++) 42 sum += (a[i] * pow(x,i)); 43 // printf("%f\n",sum); 44 return sum; 45 } 46 //方法二 47 double f2(int n, double a[], double x) { 48 double sum = a[n]; 49 for(int i = n; i > 0; i--) 50 sum = a[i-1] + x*sum; 51 // printf("%f\n",sum); 52 return sum; 53 }
标签:
原文地址:http://www.cnblogs.com/kuotian/p/5293361.html