标签:
题目所给程序代码如下:
using System; using System.Collections.Generic; using System.Text; namespace FindTheNumber { class Program { static void Main(string[] args) { int[] rg = {2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19, 20,21,22,23,24,25,26,27,28,29,30,31}; for (Int64 i = 1; i < Int64.MaxValue; i++) { int hit = 0; int hit1 = -1; int hit2 = -1; for (int j = 0; (j < rg.Length) && (hit <= 2); j++) { if ((i % rg[j]) != 0) { hit++; if (hit == 1) { hit1 = j; } else if (hit == 2) { hit2 = j; } else break; } } if ((hit == 2) && (hit1 + 1 == hit2)) { Console.WriteLine("found {0}", i); } } } } }
问题如下:
问题1:这个程序要找的是符合什么条件的数?
问题2:这样的数存在么?符合这一条件的最小的数是什么?
问题3:在电脑上运行这一程序,你估计多长时间才能输出第一个结果?时间精确到分钟(电脑:单核CPU 4.0G Hz,内存和硬盘等资源充足)。
问题4:在多核电脑上如何提高这一程序的运行效率?
自己将这个程序运行了2个小时还不出结果,然后看了一下题,果然是要求动手估算。。。
由于不知道Int64.MaxValue到底等于多少,所以我变了个小程序看了一下,如下图
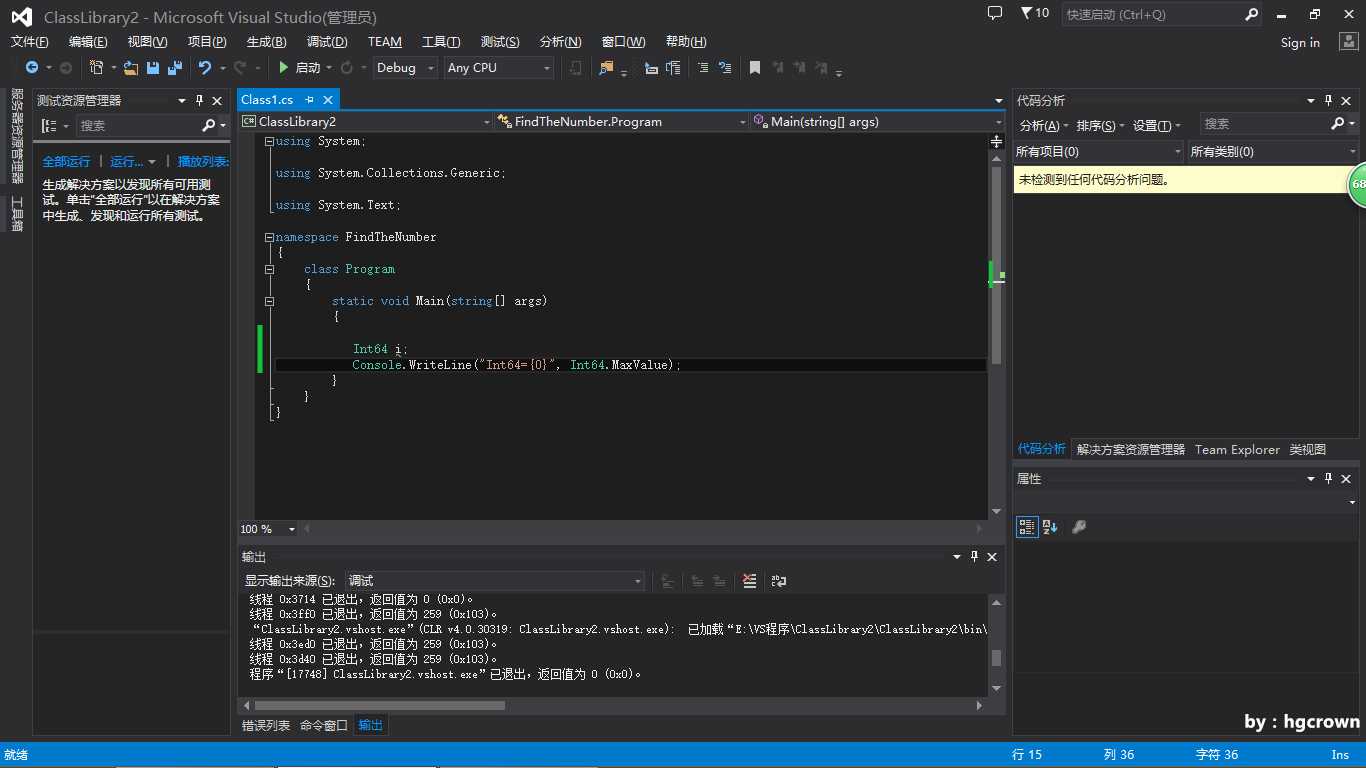
结果显示如图
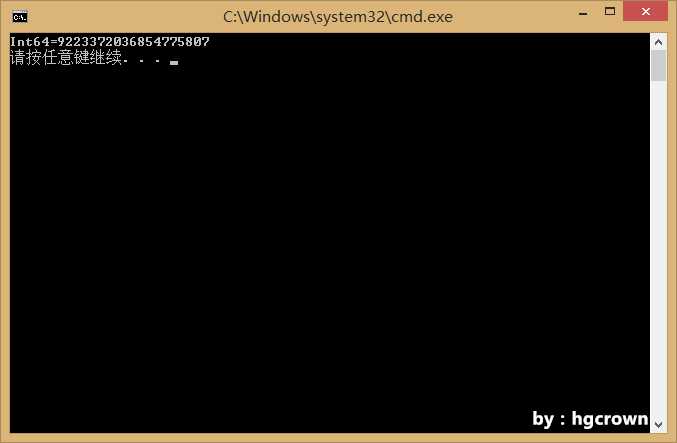
所以Int64.MaxValue=9223372036854775807=2^63-1
我的回答:
问题1:这个程序要找的是符合什么条件的数?
答:首先有两个for循环,可以明显看出第一个for循环是要找出的数,这个数的范围是从1~2^63-1,很大的范围,所以我从现在就可以估计这个时间会很长很长,而且不能运行出来,需要手动算出。其次,第二个for循环是寻找这个数的条件,从rg这个数组的第一个数开始,一直到最后一个数,if ((i % rg[j]) != 0),即寻找一个数不能整除数组中的一个数后,累加数hit+1=1,然后数组循环,寻找第二个也不能被 i 整除的数组,如果找到,hit+1=2,然后判断hit是否等于2,如果等于2,且数组中不能整除 i 的两个数相邻,且数组中其余数都能整除 i ,即寻找到此数 i 。总之,就是寻找一个数不能被数组rg中两个相邻的数整除且能被数组中其它数整除的一个数 i ,因为范围很大,所以估计不会太小!
问题2:这样的数存在么?符合这一条件的最小的数是什么?
答:因为如果大数能整除的话,那么这个数的因子,即多有组成这个大数的小数都能整除,根据这个理论的话,我的想法是从小数开始,因为小数最可能整除,所以可以最先排除,而越大的数越不容易整除,所以一个一个排除。
我的方法如下(仅代表我黄冠译个人想法,可能不对,请勿参考,o(∩_∩)o ),总体思想是分为两部分数,大数部分和小数部分:
①首先将数组分为两部分,大数和小数,数组为{2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31},其中30除以2为15,所以30能整除,则15肯定能整除,所以依据此原则2,3,4,5,6,7,8,9,10,11,12,13,14,15可以被排除,因为他们是属于小数。
②此时就剩下{16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31},下一个方法是,看组成大数的两个小数能否整除,若能则不需要大数,如不能,则大数必须存在,举个例子30由3*10组成,3和10为小数必能整除,则30肯定存在,用此方法得出,18,20,21,22,24,25,26,28,30都可以排除。
③此时剩下{16,17,19,23,27,29,31},因为素数肯定需要,所以素数整体都可以排除,且他们的乘积为基础数值。
④此时剩下{16,27},即为两个hit1,两个hit2分别为16+1=17和27+1=28,或27-1=26,因为26和28肯定能整除,所以27的相邻数不满足要求,只剩16和17.
⑤所以终于找到两个相邻数为{16,17},因为素数的乘积为基础数值,即为2*3*5*7*11*13*19*23*29*31=11797675890,如图计算器结果。
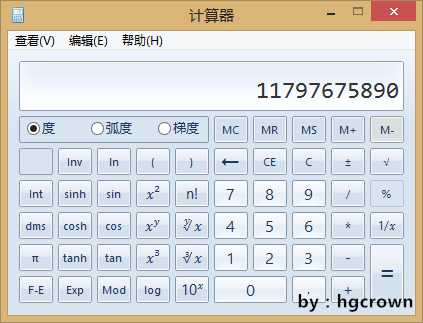
此为基础数值,需满足不能被{16,17}整除且能被其他数整除,则需继续*4*9,所以11797675890*4*9=424716332040。如图
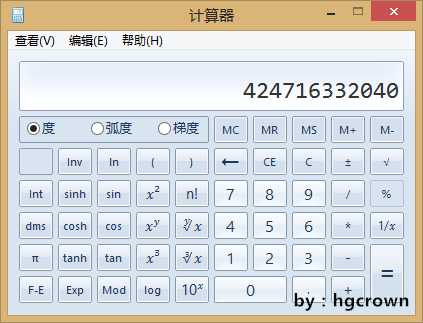
所以次数为 424716332040。
问题3:在电脑上运行这一程序,你估计多长时间才能输出第一个结果?时间精确到分钟(电脑:单核CPU 4.0G Hz,内存和硬盘等资源充足)。
答:4GHz=4*10^9Hz,每12个时钟完成一次机械周期,每个for循环大约需要12个机械周期,外层for循环了2^63-1次,外层平均最多跑16/2=8次,所以共需
[(2^63-1)*8*12*12]/[4*10^9]=2562047788015215.5022小时
不知道算的方法对不对。
我的电脑比较落伍,以下是我的电脑配置以及我用CPU-Z软件对我的CPU进行的分析的知我的CPU是4线程。
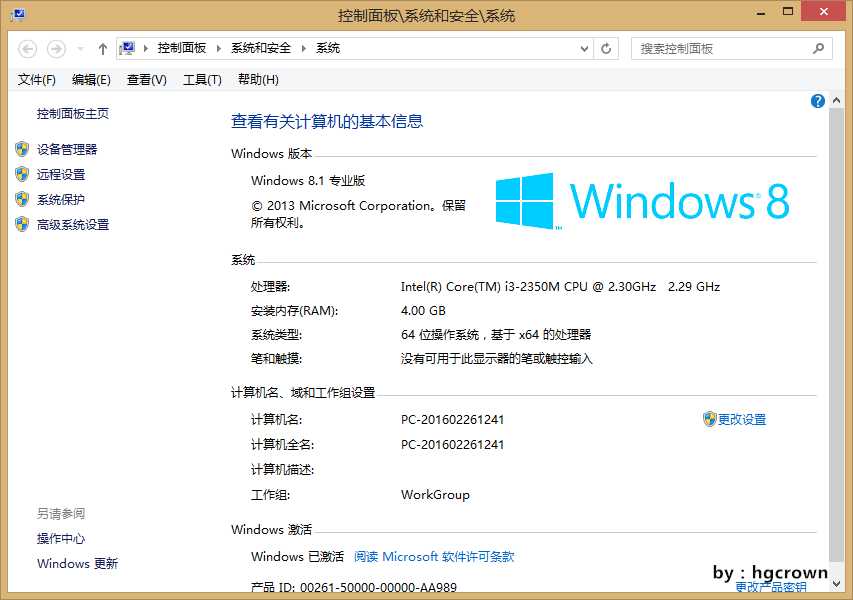
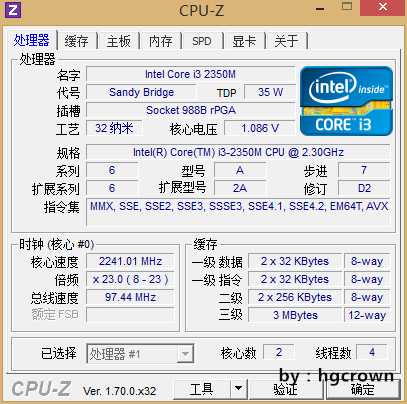
根据我的CPU,我进行了粗糙的估算:我的CPU是2.3GHz,双核4线程为假四核,我的电脑运行这个程序的时候CPU利用率如图所示
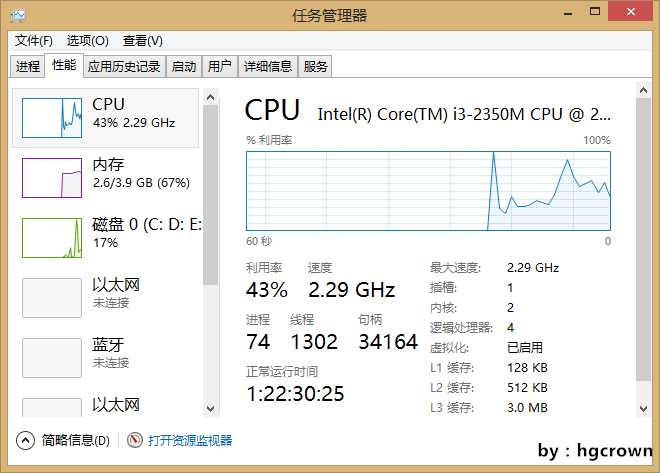
利用率最大为43%,以最快速度计算,共需:
{[(2^63-1)*8*12*12]/[2.3*10^9*4]}/43%=2685875780195.3488s=746076605.6098小时
问题4:在多核电脑上如何提高这一程序的运行效率?
答:①尽量少的启动其它应用程序占用CPU,从而使CPU可以提供更多的线程来运行这个程序,加快计算速度。
②在上图我用我的电脑做了对比,所以从硬件上提高速度,在多核情况下,提供多线程,多通道进行运算会提高速度。
总结:这次的程序考验了我们读程序的能力,首先理解程序之后,再去想结果,程序没弄明白需要干什么,完全不知道下一步需要干什么。在后面的估算中,肯定有很多地方是错误的,我也尽了自己最大的努力去计算,但是我自己的能力有限,没有做出精准计算,有很多地方的不足之处,还希望老师指点批评。
标签:
原文地址:http://www.cnblogs.com/hgcrown/p/5295402.html