逻辑回归

标签：

逻辑回归

1、  总述

　　逻辑回归来源于回归分析，用来解决分类问题，即预测值变为较少数量的离散值。

2、  基本概念

　　回归分析(Regression Analysis)：存在一堆观测资料，希望获得数据内在分布规律。单个样本表示成二维或多维向量，包含一个因变量Y和一个或多个自变量X。回归分析主要研究当自变量变化时，因变量如何变化，数学表示成Y=f(X)，其中函数f称为回归函数(regression function)。回归分析最终目的是找到最能代表已观测数据的回归函数。

　　分类：因变量Y为有限离散集，即y∈{1,2,3…}。利用训练得到的回归模型h_θ(x)进行分类，设定阈值0.5。如果h_θ(x)>=0.5，预测结果为“y=1”，相反h_θ(x)<0.5，预测结果为“y=0”。这里h_θ(x)的值可以>1 或<0。对于逻辑回归分类来说，希望0<=h_θ(x)<=1。

　　逻辑函数：也成为Sigmoid函数。线性回归中h_θ(x)=θ^Tx，显然无法限定输出到0,1之间。所以逻辑回归的Hypothesis表示为：h_θ(x)=g(θ^Tx)。这里g称为Sigmoid函数，表达式为：g(z)=1/(1+e^-z)，图形如下：

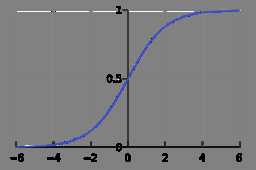
于是逻辑回归的Hypothesis最终表示为h_θ(x)=1/(1+e^-θTx)，含义是给定输入x，参数化的θ(参数空间)，输出y=1的概率。也可表示为

h_θ(x)=P(y=1|x;θ)                                                (1)

对于二分类问题，P(y=1|x;θ)+ P(y=0|x;θ)=1，所以

P(y=0|x;θ)=1- P(y=1|x;θ)                                     (2)

　　决策边界(Decision boundary)：对于h_θ(x)同样设定阈值0.5，当h_θ(x)>=0.5时，y=1，此时θ^Tx>=0。当h_θ(x)<0.5时，y=0，此时θ^Tx<0。所以可以认为θ^Tx=0是一个决策边界。

　　代价函数(Cost function)：线性回归代价函数定义为：

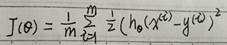
可以简写为：

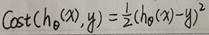
上述代价函数为凸函数，对于凸函数来说局部最小值即为全局最小值，所以只要求得一个局部极小值，该点一定为全局极小值点。将逻辑回归h_θ(x)=1/(1+e^-θTx)代入上面的代价函数，会存在问题即函数“非凸”的，所以需要引入其它代价函数。

逻辑回归代价函数定义为：

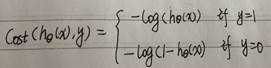
当y=1时，函数曲线如下：

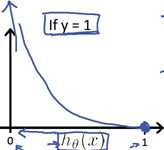
当y=1，h_θ(x)=1时，cost为0，也就是预测值与真实值完全相等时，代价为0.当h_θ(x)->0时，cost->∞。当h_θ(x)=0，也就是P(y=1|x;θ)=0，也就是预测y=1的概率为0，此时惩罚cost值趋向无穷大。

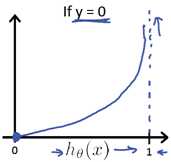
同样的，y=0情况类似。

　　简化代价函数及梯度下降求解：逻辑回归的代价函数可以简写为：

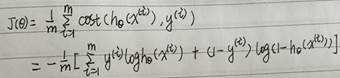
中括号中式子为对逻辑回归函数进行最大似然估计求解的最大似然函数，对最大似然函数求最大值，从而得到参数θ的估计。具体推导留到下节。这里类似，求解代价函数取的最小值时的参数θ。含义不同，实际上公示一样。与线性回归类似，可以利用梯度下降法求解参数θ。

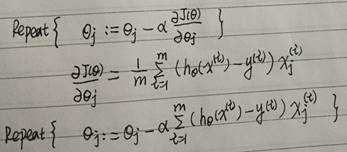
　　优化求解算法：共轭梯度(Conjugate gradient)、BFGS、L-BFGS算法。优点是不需要人工挑选学习步长α，通常速度比梯度下降法快。缺点通常更复杂。

3、  算法求解

　　最大似然估计求解：综合式(1)和式(2)得到概率函数为：

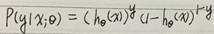
似然函数为：

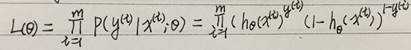
对数似然函数为：

可以看出代价函数J(θ)=-l(θ)/m。利用梯度上升法求对数似然函数取最大值的参数θ，等价于梯度下降法求代价函数J取最小值时的参数θ。

　　梯度下降法求解：

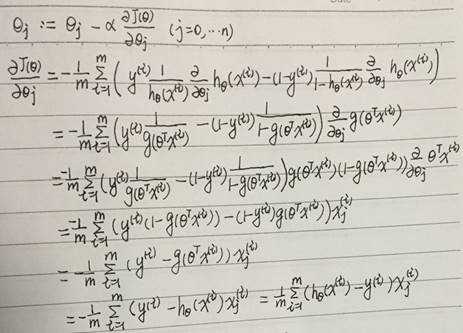
其中，用到了下面的求导公示：

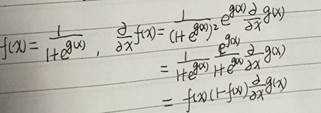
最终结果为：

4、  附录

　　代价函数：监督学习问题是在假设空间F中选取模型f作为决策函数，对于给定的输入X，由f(X)给出相应的输出Y，这个输出的预测值f(X)与真实Y可能不一致。用一个损失函数(loss function)或代价函数(cost function)来度量预测错误的程度。损失函数是f(x)和Y的非负实值函数，记做L(Y, f(X))。

参考

http://ilanever.com/article/detail.do;jsessionid=9A6E0C3D33ECADD6723113777AA6DE9C?id=260

http://52opencourse.com/125/coursera公开课笔记-斯坦福大学机器学习第六课-逻辑回归-logistic-regression

李航：《统计学习方法》

http://blog.csdn.net/dongtingzhizi/article/details/15962797

http://blog.jasonding.top/2015/01/09/Machine%20Learning/【机器学习基础】Logistic回归基础

http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971867.html

逻辑回归

标签：

原文地址：http://www.cnblogs.com/wmymartin/p/5303778.html