标签:
题目:http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=20416
这道题几乎是纯的“凸包问题”,也让我对于凸包有了入门级的认识。
我看到的比较好的算法是Graham扫描法,用笔模拟了一下该算法,大致就对该算法有所体会了,所以碰到一个新算法,一定要不怕麻烦,通过模拟该算法深入了解其中的奥秘
Graham扫描法的具体流程:
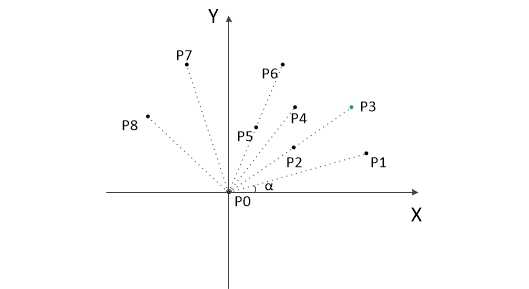
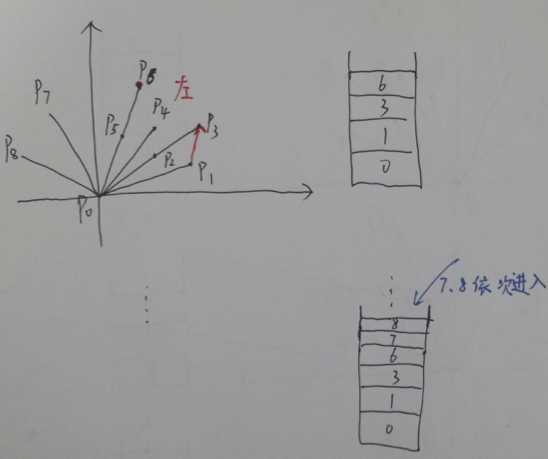
1. 首先确定所有点中的y值最小的点P0(如果有多个点,任取一个就好)。显然,P0一定是构成凸包的点
2. 以P0为原点,将其他的点P1~P8根据极角大小(极角相等的点,按照点到P0的距离升序排序),升序排序(O(nlgn))。根据几何知识可知,极角最小的点(如上图P1)和极角最大的点(如上图P8)一定是构成凸包的点。
3. 准备一个空的栈S,让P0,P1入栈,然后开始遍历P2~P8。假设当前遍历到P2(当前点),那么就将栈顶的两个元素取出(P0和P1),如果当前点P2位于向量P0指向P1的左侧(或在直线上,这个可以自己定),那么就将P2入栈;否则,不断让栈顶元素出栈直到P2位于 栈顶两个元素构成的向量 的左侧。(O(n))
整体时间复杂度:O(nlgn)
附:对于上图样例,算法每一步的过程:
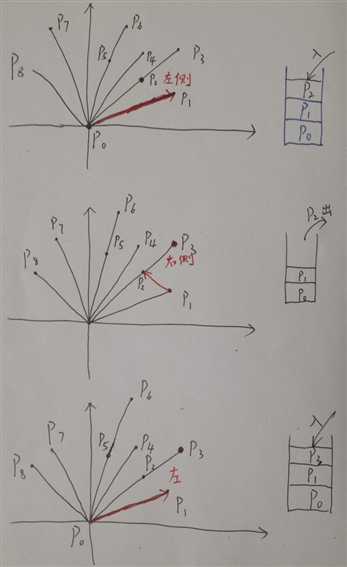
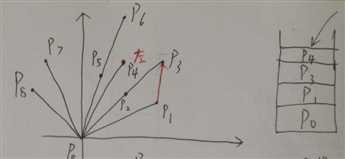
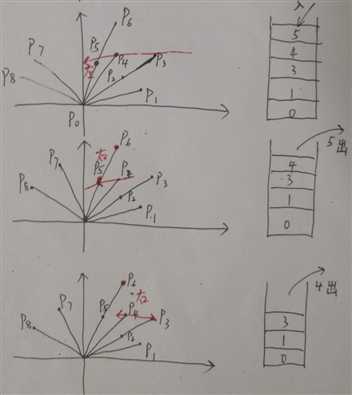
#include <cstdio> #include <iostream> #include <cmath> #include <algorithm> using namespace std; struct Point { int x, y; Point(int x=0, int y=0):x(x),y(y) {} } p[105]; typedef Point Vector; Vector operator - (Point a, Point b) { return Vector(a.x-b.x, a.y-b.y); } // 叉乘 double Cross(Vector a, Vector b) { return a.x*b.y - a.y*b.x; } // 确定浮点数的符号性质(+, -, 0) const double EPS = 1e-10; int dcmp(double x) { if(fabs(x) < EPS) return 0; return x < 0 ? -1 : 1; } double Dist(Point a, Point b) { return sqrt((double)(a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y)); } bool cmp(Point a, Point b) // 用于极角排序 { Vector u = a-p[0], v = b-p[0]; int sign = dcmp(Cross(u, v)); if(sign == 0) return Dist(a, p[0]) < Dist(b, p[0]); return sign > 0; } double grahamscan(Point *a, int n) { if(n == 1) return 0; // 这里zoj和hdu有不同,zoj认为要乘2,hdu认为不乘,有点坑 if(n == 2) return 2*Dist(a[0], a[1]); int *st = new int[n]; int j=0; st[j++] = 0; st[j++] = 1; st[j++] = 2; for(int i=3; i<n; i++) { // 这里可以取到 等于,减少不必要的距离计算 while(dcmp(Cross(a[st[j-1]]-a[st[j-2]], a[i]-a[st[j-2]])) <= 0) --j; st[j++] = i; } double ret = 0.0; for(int i=1; i<j; i++) { ret += Dist(a[st[i-1]], a[st[i]]); } return ret + Dist(a[st[0]], a[st[j-1]]); } int main () { int n; while(scanf("%d", &n) != EOF && n) { int mini, miny=32767+10; for(int i=0; i<n; i++) { scanf("%d%d", &p[i].x, &p[i].y); if(miny > p[i].y) { miny = p[i].y; mini = i; } } swap(p[0], p[mini]); sort(p+1, p+n, cmp); printf("%.2lf\n", grahamscan(p, n)); } return 0; }
ZOJ - 1453 —— Surround the Trees (求凸包长度)
标签:
原文地址:http://www.cnblogs.com/AcIsFun/p/5323665.html