标签:
写在前面:
二叉树是比较简单的一种数据结构,理解并熟练掌握其相关算法对于复杂数据结构的学习大有裨益
一.二叉树的创建
所谓的创建二叉树,其实就是让计算机去存储这个特殊的数据结构(特殊在哪里?特殊在它是我们自定义的)
首先,计算机内部存储都是线性的,而我们的树形结构是一种层级的,计算机显然无法理解,计算机能够接受的原始数据类型并不能满足我们的需求
所以,只好自定义一种数据结构来表示层级关系
实际上是要定义结构 + 操作,结构是为操作服务的,举个例子,我们要模拟买票的过程,现有的数据结构无法满足我们的需求(不要提数组...),我们需要的操作可能是:
1.获取站在买票队伍最前面的人
2.把买好票的人踢出队伍
3.第一个人买完票后,他后面的所有人都要“自觉”地向前移动
明确了这三个操作,再根据操作来定义结构,最后我们得到了队列(数组/链表 + 对应的函数)
二叉树也是这样,计算机看到的只是结构 + 操作,结构是Node集合(二叉链表),操作是创建、遍历、查找等等函数
结点:
struct bt
{
char data;
struct bt *left;
struct bt *right;
};
结点就是一个桶,两只手(桶里装数据,两只手伸出去抓左右两个孩子)
操作:
//createBT(); //printBT(); //deleteNode(Node node); //...
-------上面是对二叉树的理解,下面是创建二叉树具体实现-------
二叉树的创建过程其实就是遍历过程(此处指递归方式),我们知道二叉树的任何一种遍历方式都可以把树形结构线性化(简单的说就是一组遍历结果可以唯一的表示一颗二叉树),因此可以根据遍历结果来还原一颗二叉树
先序遍历递归建树的具体思路:
1.读入当前根结点的数据
2.如果是空格,则将当前根置为空,否则申请一个新结点,存入数据
3.用当前根结点的左指针和右指针进行递归调用,创建左右子树
语言描述可能不太好懂,代码如下:
struct bt
{
char data;
struct bt *left;
struct bt *right;
};
void createBT(struct bt ** root)
{
char c;
c=getchar();
if(c == ‘ ‘)*root=NULL;//若为空格则置空
else
{
*root=(struct bt *)malloc(sizeof(struct bt));//申请新结点
(*root)->data=c;//存入数据
createBT(&((*root)->left));//建立当前结点的左子树
createBT(&((*root)->right));//建立当前结点的右子树
}
}
例如,如果我们要建立一个二叉树a(b, c),只要输入它的先序遍历结果ab××c××即可(×表示空格),其余两种建树方式于此类似,不再详述,至于非递归的建树方法参见下面的非递归遍历,非常相似
二.遍历
遍历在实现方式上有递归与非递归两种方式,所谓的非递归其实是由递归转化而来的(手动维护一个栈),开销(内存/时间)上可能非递归的更好一些,毕竟操作系统的栈中维护的信息更多,现场的保存与恢复开销都要更大一些
在遍历顺序上有3种方式:
1.先序遍历(根-左-右)
2.中序遍历(左-根-右)
3.后序遍历(左-右-根)
举个例子,二叉树a(b, c(d, e))的三种遍历结果分别是:
1.abcde
2.badce
3.bdeca
-------下面看看后序遍历的递归与非递归实现,其余的与之类似-------
后序遍历递归:
void postOrder(struct bt * root)
{
if(root == NULL)return;
else
{
postOrder(root->left);
postOrder(root->right);
putchar(root->data);
}
}
后序遍历非递归:
void postOrder(struct st* root)
{
struct st* stack[100];//声明结点栈
int top=-1;//栈顶索引
struct bt* p=root;//当前结点(present)
struct bt* q=NULL;//上一次处理的结点
while(p!=NULL||top!=-1)
{
for(;p!=NULL;p=p->left)stack[++top]=p;//遍历左子树
if(top!=-1)
{
p=stack[top];
if(p->right==NULL||p->right==q)//无右孩子,或右孩子已经遍历过
{
putchar(p->data);//输出根结点
q=p;
p=stack[top];
top--;
p=NULL;
}
else p=p->right;//遍历右子树
}
}
}
为了描述地更清晰,上面直接实现了栈的操作,当然,更规范的做法是将栈作为一个独立的数据结构封装起来,在我们的函数中调用栈提供的操作函数来进行相关操作
三.输出叶结点
检索特定结点的一系列操作都是建立在遍历的基础上的,输出叶结点就是一个例子,叶结点满足的条件是左右孩子都为空,我们只要在遍历中添加这样的判断条件就可以了
//此处采用先序遍历
void printLeaves(struct bt* root)
{
if(root == NULL)return;
else
{
if(root->left == NULL&&root->right == NULL)putchar(root->data);
else
{
printLeaves(root->left);
printLeaves(root->right);
}
}
}
于此类似的操作有,输出二叉树中满足一定条件的结点,删除指定结点,在指定位置添加结点(子树)...都是在遍历的基础上做一些额外的操作
四.计算树的深度
计算树深有多种方式,例如:
1.分别计算根下左右子树的高度,二者中的较大的为树深
2.最大递归深度为树深
...
我们采用第一种方式,更清晰一些
int btDepth(struct bt* root)
{
int rd,ld;
if(root==NULL)return 0;//空树深度为0
else
{
ld=1+btDepth(root->left);//递归进层,深度加1
rd=1+btDepth(root->right);//递归进层,深度加1
return ld > rd ? ld : rd;//返回最大值
}
}
五.树形输出
所谓树形输出,即对自然表示的二叉树逆时针旋转90度,其实仍然是在遍历的过程中记录递归层数,以此确定输出结果
//depth表示递归深度,初始值为0
void btOutput(struct bt* root,int depth)
{
int k;
if(root==NULL)return;
else
{
btOutput(root->right,depth+1);//遍历右子树
for(k=0;k<depth;k++)
printf(" ");//递归层数为几,就输出几个空格(缩进几位)
putchar(root->data);printf("\n");
btOutput(root->left,depth+1);//遍历左子树
}
}
//“右-中-左”的遍历顺序被称为“逆中序”遍历,采用这种顺序是为了符合输出规则(逆时针90度)
六.按层缩进输出
按层缩进输出就像代码编辑器中的自动缩进,从根结点开始逐层缩进,只需要对上面的代码稍作改动就可以实现
//k仍然表示递归深度,初始值为0
void indOutput(struct bt* root,int k)
{
int i;
if(root!=NULL)
{
for(i=1;i<=k;i++)
putchar(‘ ‘);
putchar(root->data);putchar(‘\n‘);
indOutput(root->left,k+1);
indOutput(root->right,k+1);
}
else return;
}
//按层缩进输出与树形输出的唯一区别就是遍历方式不同,前者是先序遍历,后者是逆中序遍历
七.按层顺序输出
按层顺序输出与前面提及的两种输出方式看似相似,实则有着很大不同,至少,我们无法简单地套用任何一种遍历过程来完成这个目标
所以,只能维护一个队列来控制遍历顺序
void layerPrint(struct bt* root)
{
struct bt* queue[100];//声明结点队列
struct bt* p;//当前结点
int amount=0,head,tail,j,k;//队列相关属性(元素总数,对头、队尾索引)
queue[0]=root;
head=0;
tail=1;
amount++;
while(1)
{
j=0;
for(k=0;k<amount;k++)
{
p=queue[head++];//取对头元素
if(p->left!=NULL)
{
queue[tail++]=p->left;//如果有则记录左孩子
j++;
}
if(p->right!=NULL)
{
queue[tail++]=p->right;//如果有则记录右孩子
j++;
}
putchar(p->data);//输出当前结点值
}
amount=j;//更新计数器
if(amount==0)break;
}
}
八.计算从根到指定结点的路径
要记录路径,当然不宜用递归的方式,这里采用后序遍历的非递归实现
为什么选择后序遍历?
因为在这种遍历方式中,某一时刻栈中现有的结点恰恰就是从根结点到当前结点的路径(从栈底到栈顶)。严格地说,此时应该用队列来保存路径,因为栈不支持从栈底到栈顶的出栈操作(这样的小细节就把它忽略好了...)
//参数c为指定结点值
void printPath(struct bt* root,char c)
{
struct st* stack[100];//声明结点栈
int top=-1;//栈顶索引
int i;
struct bt* p=root;//当前结点
struct bt* q=NULL;//上一次处理的结点
while(p!=NULL||top!=-1)
{
for(;p!=NULL;p=p->left)stack[++top]=p;//遍历左子树
if(top!=-1)
{
p=stack[top];//获取栈顶元素
if(p->right==NULL||p->right==q)//如果当前结点没有右孩子或者右孩子刚被访问过
{
if(p->data==c)//如果找到则输出路径
{
for(i=0;i<=top;i++)
{
p=stack[i];
putchar(p->data);
}
printf("\n");
//此处不跳出循环,因为可能存在不唯一的结点值,遍历整个树,找出所有路径
}
q=p;
p=stack[top];
top--;
p=NULL;
}
else p=p->right;//遍历右子树
}
}
}
九.完整源码与截图示例
源码:
#include<stdio.h>
struct bt
{
char data;
struct bt *left;
struct bt *right;
};
void createBT(struct bt ** root)
{
char c;
c=getchar();
if(c == ‘ ‘)*root=NULL;
else
{
*root=(struct bt *)malloc(sizeof(struct bt));
(*root)->data=c;
createBT(&((*root)->left));
createBT(&((*root)->right));
}
}
void preOrder(struct bt * root)
{
if(root == NULL)return;
else
{
putchar(root->data);
preOrder(root->left);
preOrder(root->right);
}
}
void inOrder(struct bt * root)
{
if(root == NULL)return;
else
{
inOrder(root->left);
putchar(root->data);
inOrder(root->right);
}
}
void printLeaves(struct bt* root)
{
if(root == NULL)return;
else
{
if(root->left == NULL&&root->right == NULL)putchar(root->data);
else
{
printLeaves(root->left);
printLeaves(root->right);
}
}
}
int btDepth(struct bt* root)
{
int rd,ld;
if(root==NULL)return 0;
else
{
ld=1+btDepth(root->left);
rd=1+btDepth(root->right);
return ld > rd ? ld : rd;
}
}
void btOutput(struct bt* root,int depth)
{
int k;
if(root==NULL)return;
else
{
btOutput(root->right,depth+1);
for(k=0;k<depth;k++)
printf(" ");
putchar(root->data);printf("\n");
btOutput(root->left,depth+1);
}
}
void postOrder(struct st* root)
{
struct st* stack[100];
int top=-1;
struct bt* p=root;
struct bt* q=NULL;
while(p!=NULL||top!=-1)
{
for(;p!=NULL;p=p->left)stack[++top]=p;
if(top!=-1)
{
p=stack[top];
if(p->right==NULL||p->right==q)
{
putchar(p->data);
q=p;
p=stack[top];
top--;
p=NULL;
}
else p=p->right;
}
}
}
void printPath(struct bt* root,char c)
{
struct st* stack[100];
int top=-1;
int i;
struct bt* p=root;
struct bt* q=NULL;
while(p!=NULL||top!=-1)
{
for(;p!=NULL;p=p->left)stack[++top]=p;
if(top!=-1)
{
p=stack[top];
if(p->right==NULL||p->right==q)
{
if(p->data==c)
{
for(i=0;i<=top;i++)
{
p=stack[i];
putchar(p->data);
}
printf("\n");
}
q=p;
p=stack[top];
top--;
p=NULL;
}
else p=p->right;
}
}
}
void layerPrint(struct bt* root)
{
struct bt* queue[100];
struct bt* p;
int amount=0,head,tail,j,k;
queue[0]=root;
head=0;
tail=1;
amount++;
while(1)
{
j=0;
for(k=0;k<amount;k++)
{
p=queue[head++];
if(p->left!=NULL)
{
queue[tail++]=p->left;
j++;
}
if(p->right!=NULL)
{
queue[tail++]=p->right;
j++;
}
putchar(p->data);
}
amount=j;
if(amount==0)break;
}
}
void indOutput(struct bt* root,int k)
{
int i;
if(root!=NULL)
{
for(i=1;i<=k;i++)
putchar(‘ ‘);
putchar(root->data);putchar(‘\n‘);
indOutput(root->left,k+1);
indOutput(root->right,k+1);
}
else return;
}
void main()
{
char c;
struct bt * root;
printf("请输入先序遍历结果: ");
createBT(&root);
printf("先序遍历(preOrder)[递归]: \n");
preOrder(root);
printf("\n中序遍历(inOrder)[递归]: \n");
inOrder(root);
printf("\n后序遍历(postOrder)[非递归]: \n");
postOrder(root);
printf("\n叶结点(leaves): \n");
printLeaves(root);
printf("\n深度(depth): \n");
printf("%d\n",btDepth(root));
printf("树形输出(tree output): \n");
btOutput(root,0);
printf("缩进输出(indentation output): \n");
indOutput(root,0);
printf("请输入目标结点(target node): ");
getchar();
c=getchar();
printf("路径(path): \n");
printPath(root,c);
printf("按层输出(layerPrint): \n");
layerPrint(root);
printf("\n");
}
截图示例:
一颗较为复杂的二叉树:
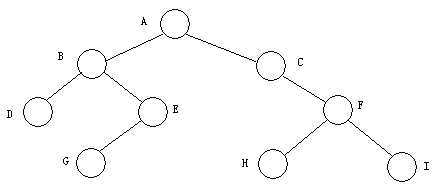
其先序遍历结果为:ABD××EG×××C×FH××I××(×表示空,输入的时候要把×换成空格)
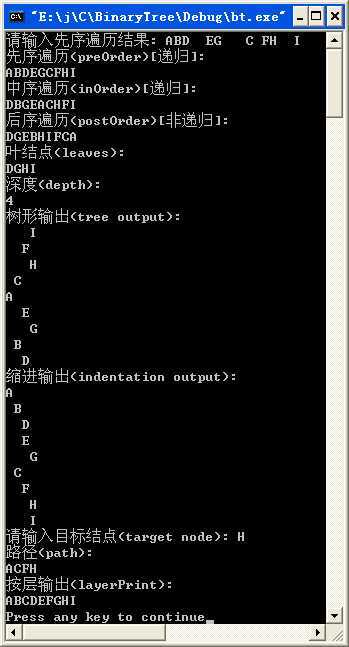
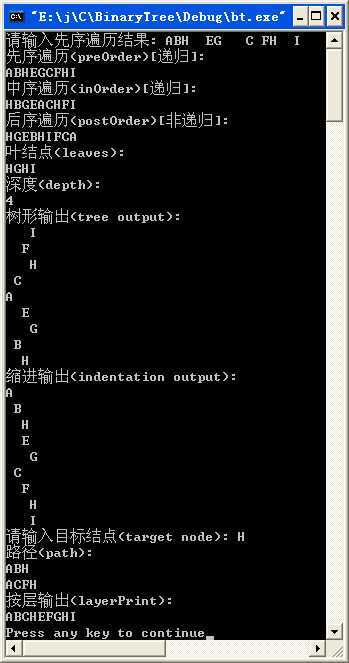
把D改成H再试一次(存在重复元素了,因该有两条到H的路径)
标签:
原文地址:http://www.cnblogs.com/ayqy/p/3871276.html