Stanford机器学习---第八讲. 支持向量机SVM

标签：

本文原始文章见http://blog.csdn.net/abcjennifer/article/details/7849812，本文添加了一些自己的理解

本栏目（Machine learning）包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM（Support Vector Machines 支持向量机）、聚类、降维、异常检测、大规模机器学习等章节。所有内容均来自Standford公开课machine learning中Andrew老师的讲解。（https://class.coursera.org/ml/class/index）

第八讲. 支持向量机进行机器学习——Support Vector Machine

===============================

（一）、SVM 的 Cost Function

（二）、SVM —— Large Margin Classifier

（三）、数学角度解析为什么SVM 能形成 Large Margin Classifier（选看）

（四）、SVM Kernel 1 —— Gaussian Kernel

（五）、SVM 中 Gaussian Kernel 的使用

(六)、SVM的使用与选择

本章内容为支持向量机Support Vector Machine（SVM）的导论性讲解，在一般机器学习模型的理解上，引入SVM的概念。原先很多人，也包括我自己觉得SVM是个很神奇的概念，读完本文你会觉得，其实只是拥有不同的目标函数， 不同的模型而已，Machine Learning的本质还没有变，呵呵~

完成本文花了我很长时间，为了搞懂后面还有程序方便和参考网站大家实验，希望对大家有所帮助。

=====================================

（一）、SVM 的 Cost Function

前面的几章中我们分别就linear regression、logistic regression以及神经网络的cost function进行了讲解。这里我们通过logistic regression的cost function引入SVM。

首先回忆一下logistic regression的模型：

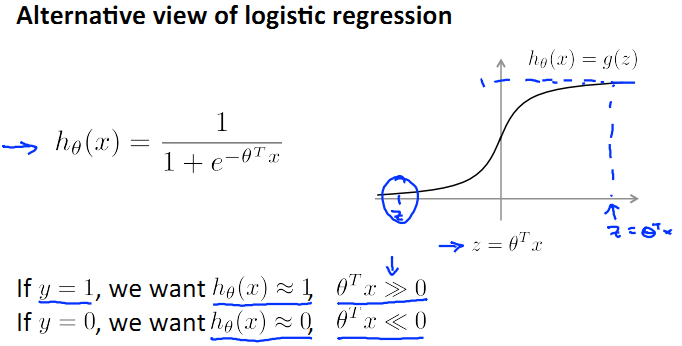
还是原先的假设，suppose我们只有两个类，y=0和y=1。那么根据上图h(x)的图形我们可以看出，

当y=1时，希望h(x)≈1，即z>>0；

当y=0时，希望h(x)≈0，即z<<0；

那么逻辑回归的cost function公式如下：

cost function我们之前已经讲过了，这里不予赘述。现在呢，我们来看看下面的两幅图，这两幅图中灰色的curve是logistic regression的cost function分别取y=1和y=0的情况，

y=1时，随着z↑，h(x)逐渐逼近1，cost逐渐减小。

y=0时，随着z↓，h(x)逐渐逼近0，cost逐渐减小。

这正是图中灰色曲线所示的曲线。

ok，现在我们来看看SVM中cost function的定义。请看下图中玫瑰色的曲线，这就是我们希望得到的cost function曲线，和logistic regression的cost function非常相近，但是分为两部分，下面呢，我们将对这个cost function进行详细讲解。

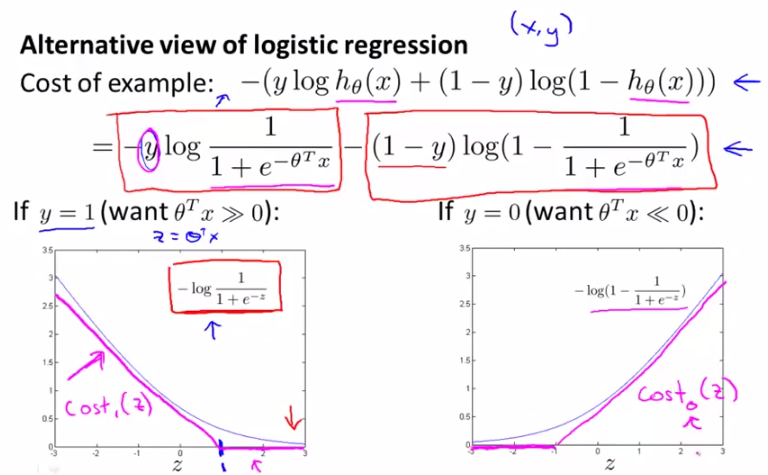
logistic regression的cost function:

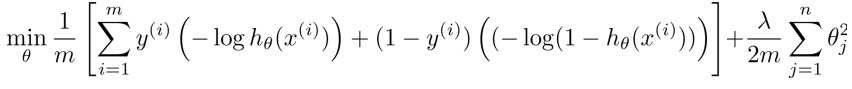
现在呢，我们给出SVM的目标函数（cost function）定义：

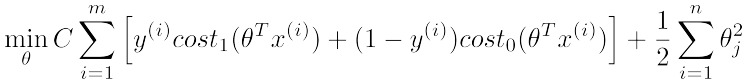
该式中，cost0和cost1分别对应y=0和y=1时的目标函数定义，最后一项regularization项和logistic regression中的类似。感觉系数少了什么？是的，其实它们的最后一项本来是一样的，但是可以通过线性变换化简得到SVM的归一化项。

=====================================

（二）、SVM —— Large Margin Classifier

本节给出一个简单的结论——SVM是一个large margin classifier。什么是margin呢？下面我们做详细讲解，其理论证明将在下一节中给出。

在引入margin之前，我们回顾一下上一节中的SVM cost function curve，如下图所示分别是y取1和0时的情况。先给出一个结论，常数C取一个很大的值比较好（比如100000），这是为什么呢？

我们来看哈，C很大，就要求[]中的那部分很小（令[]中的那部分表示为W），不如令其为0，这时来分析里面的式子：

※需求1：

y=1时，W只有前一项，令W=0，就要求Cost₁(θ^Tx)=0，由右图可知，这要求θ^Tx>=1；

y=0时，W只有后一项，令W=0，就要求Cost₀(θ^Tx)=0，由右图可知，这要求θ^Tx<=-1；

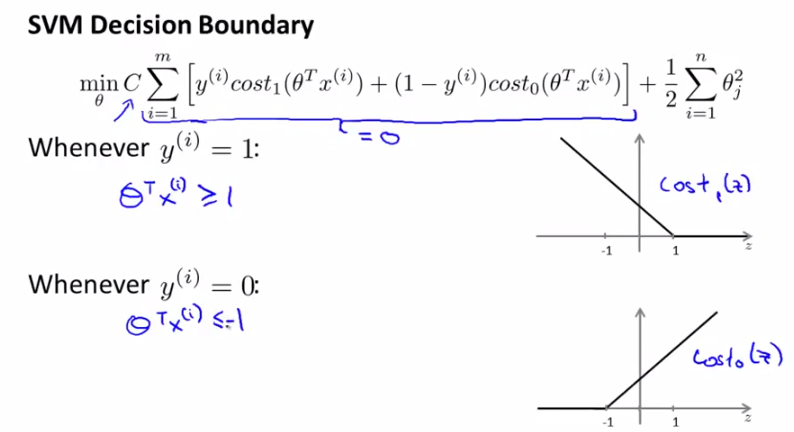
由以上说明可知，对C的取值应该在分类是否犯错和margin的大小上做一个平衡。那么C取较大的值会带来什么效果呢？就是我们开头说的结论——SVM是一个large margin classifier。那么什么是margin？在第三章中我们已经讲过了decision boundary，它是能够将所有数据点进行很好地分类的h(x)边界。如下图所示，我们可以把绿线、粉线、蓝线或者黑线中的任意一条线当做decision boundary，但是哪一条最好呢？这里我们可以看出，绿色、粉色、蓝色这三类boundary离数据非常近，i.e.我们再加进去几个数据点，很有可能这个boundary就能很好的进行分类了，而黑色的decision boundary距离两个类都相对较远，我们希望获得的就是这样的一个decision boundary。margin呢，就是将该boundary进行平移所得到的两条蓝线的距离，如图中所指。

相对比：

C小，decision boundary则呈现为黑线；若C很大，就呈现粉线；

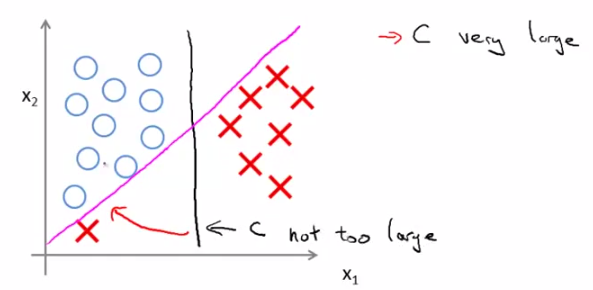
这个结论大家可以记住，也可以进行数学上的分析，下一节中我们将从数学角度分析，为什么SVM选用大valeu的C会形成一个large margin classifier。

我们可以为分错的点加上一点惩罚，对一个分错的点的惩罚函数就是这个点到其正确位置的距离：

在上图中，蓝色、红色的直线分别为支持向量所在的边界，绿色的线为决策函数，那些紫色的线表示分错的点到其相应的决策面的距离，这样我们可以在原函数上面加上一个惩罚函数，并且带上其限制条件为：

公式中蓝色的部分为在线性可分问题的基础上加上的惩罚函数部分，当xi在正确一边的时候，ε=0，R为全部的点的数目，C是一个由用户去指定的系数，表示对分错的点加入多少的惩罚，当C很大的时候，分错的点就会更少，但是过拟合的情况可能会比较严重，当C很小的时候，分错的点可能会很多，不过可能由此得到的模型也会不太正确，所以如何选择C是有很多学问的，不过在大部分情况下就是通过经验尝试得到的。

接下来就是同样的，求解一个拉格朗日对偶问题，得到一个原问题的对偶问题的表达式：

蓝色的部分是与线性可分的对偶问题表达式的不同之处。在线性不可分情况下得到的对偶问题，不同的地方就是α的范围从[0, +∞)，变为了[0, C]，增加的惩罚ε没有为对偶问题增加什么复杂度。

任意一个点x到分类平面的距离γ的表示如上图所示，其中y是{+1，-1}表示分类结果，x0是分类面上距x最短的点，分类平面的方程为wx+b=0,将x0带入该方程就有上面的结果了。对于一个数据集x，margin就是这个数据及所有点的margin中离hyperplane最近的距离，SVM的目的就是找到最大margin的hyperplane。

练习：

=====================================

（三）、数学角度解析为什么SVM 能形成 Large Margin Classifier（选看）

首先我们来看两个向量内积的表现形式。假设向量u，v均为二维向量，我们知道u，v的内积u^Tv=u₁v₁+u₂v₂。表现在坐标上呢，就如下图左边所示：

首先将v投影至u向量，记其长度为p（有正负，与u同向为正，反相为负，标量），则两向量的内积u^Tv = ||u|| · ||v|| · cosθ = ||u|| · p = u₁v₁+u₂v_2。

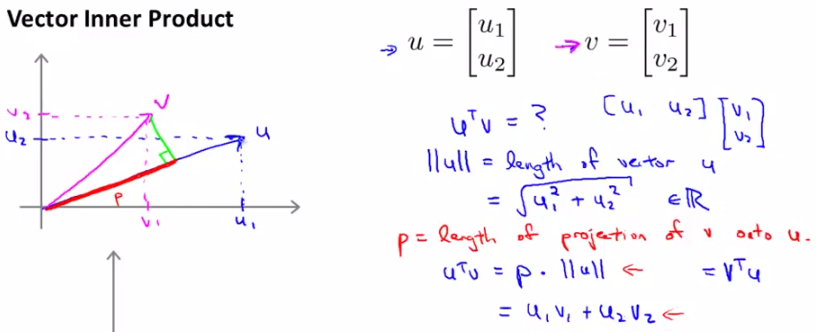
这样一来，我们来看SVM的cost function：

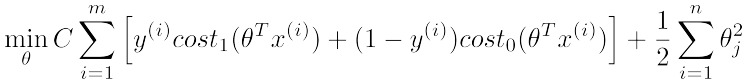
由于将C设的很大，cost function只剩下后面的那项。采取简化形式，意在说明问题即可，设θ₀=0，只剩下θ₁和θ₂，

则cost function J(θ)=1/2×||θ||^2

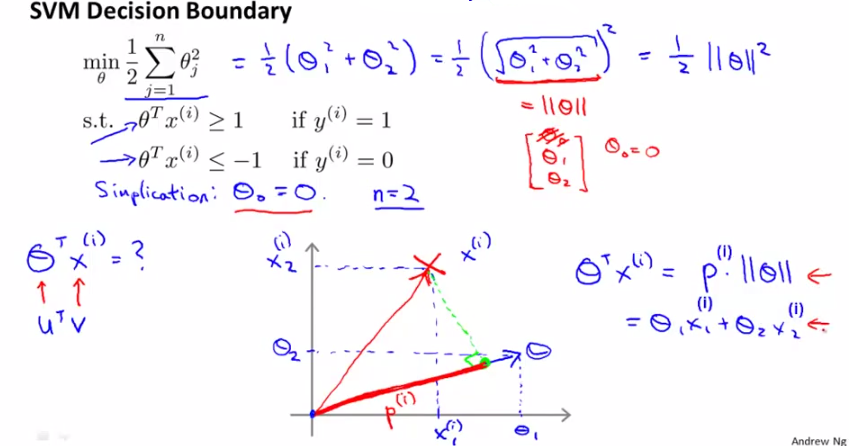
而根据上面的推导，有θ^Tx=p·||θ||，其中p是x在θ上的投影，则

※需求2：

y=1时，W只有前一项，令W=0，就要求Cost₁(θ^Tx)=0，由右图可知，这要求p·||θ||>=1；

y=0时，W只有后一项，令W=0，就要求Cost₀(θ^Tx)=0，由右图可知，这要求p·||θ||<=-1；

我们集中精力看为什么SVM的decision boundary有large margin（这里稍微有点儿复杂，好好看哈）：

对于一个给定数据集，依旧用X表示正样本，O表示负样本，绿色的线表示decision boundary，蓝色的线表示θ向量的方向，玫瑰色表示数据在θ上的投影。

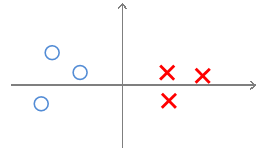
我们已知boundary的角度和θ向量呈的是90°角（自己画一下就知道了）。

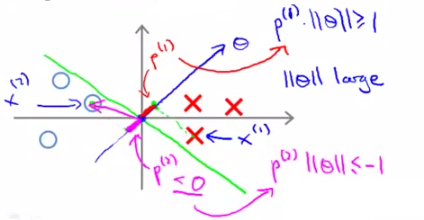
先看这个图，对于这样一个decision boundary（没有large margin），θ与其呈90°角如图所示，这样我们可以画出数据集X和O在θ上的投影，如图所示，非常小；如果想满足[需求2]中说的

对正样本p·||θ||>=1，

对负样本p·||θ||<=-1，

就需要令||θ||很大，这就和cost function的愿望（min 1/2×||θ||^2）相违背了，因此SVM的不出来这个图中所示的decision boundary结果。

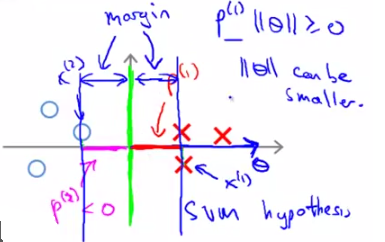
那么再来看下面这个图，

它选取了上一节中我们定义的“比较好的”decision boundary，两边的margin都比较大。看一下两边数据到θ的投影，都比较大，这样就可以使||θ||相对较小，满足SVM的cost function。因此按照SVM的cost function进行求解（optimization）得出的decision boundary一定是有large margin的。说明白了吧？！

练习：

分析：由图中我们可以看出，decision boundary的最优解是y=x1，这时所有数据集中的数据到θ上的投影最小值为2，换言之，想满足

对正样本p·||θ||>=1，

对负样本p·||θ||<=-1，

只需要

对正样本2·||θ||>=1，

对负样本（-2）·||θ||<=-1，

=====================================

（四）、SVM Kernel 1 —— Gaussian Kernel

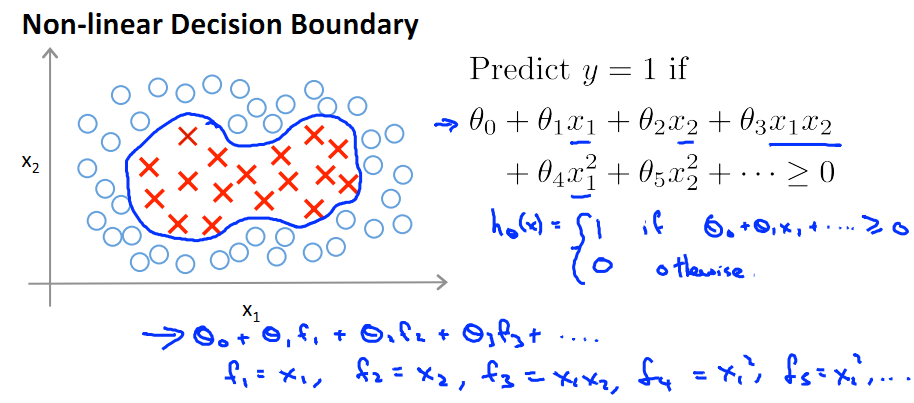
对于一个非线性Decision boundary，我们之前利用多项式拟合的方法进行预测：

• f1, f2, ... fn为提取出来的features。
• 定义预测方程h_θ(x)为多项式的sigmod函数值：h_θ(x)=g(θ₀f₀+θ₁f₁+…+θ_nf_{n)，其中fn为x的幂次项组合（如下图）}
• 当θ₀f₀+θ₁f₁+…+θ_nf_n>=0时h_θ(x)=1；else h_θ(x)=0；

那么，除了将fn定义为x的幂次项组合，还有没有其他方法表示 f 呢？本节就引入了Kernel，核的概念。即用核函数表示f。

发现相似度计算公式很像正态分布（高斯分布）对不对？是的！这就是高斯核函数。由下图可以看出，

x和l越相似，f越接近于1；

x与l相差越远，f越接近于0；

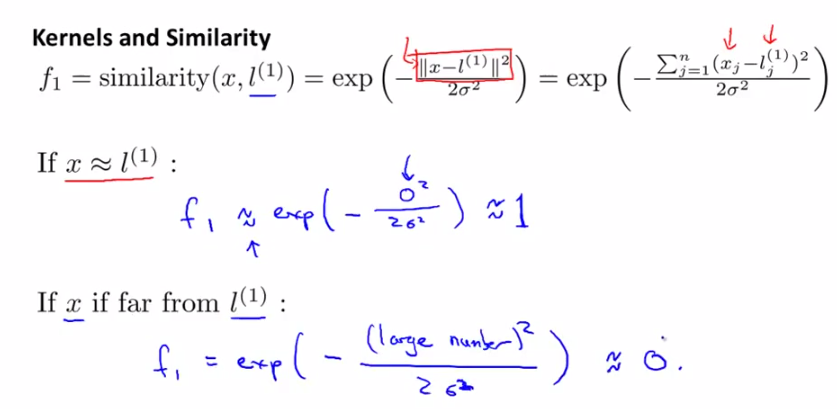
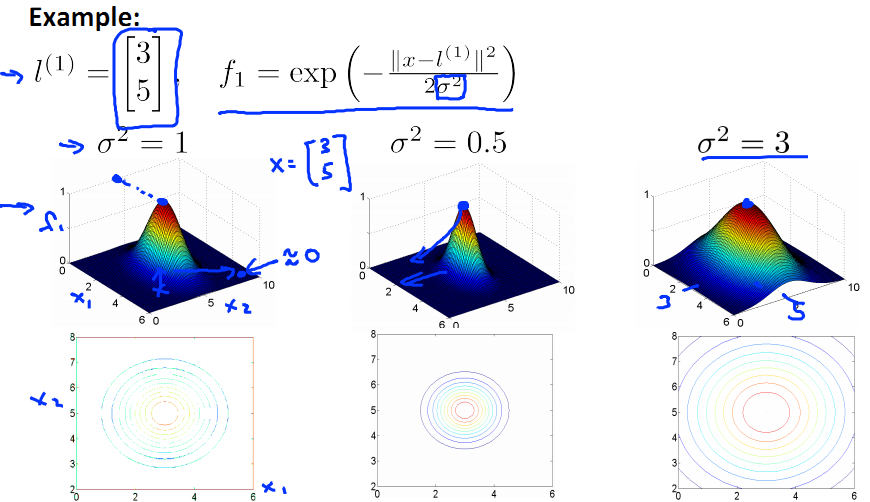
下图中的横纵坐标为x的两个维度值，高为f（new feature）。制高点为x=l的情况，此时f=1。

随着x与l的远离，f逐渐下降，趋近于0.

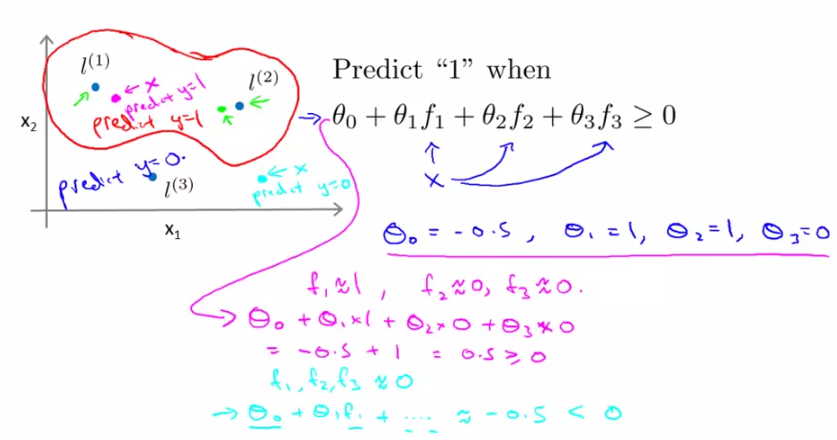
下面我们来看SVM核分类预测的结果：

引入核函数后，代数上的区别在于f变了，原来f是x1/x1^2/...，即xi幂次项乘积

引入核函数后，几何上来说可以更直观的表示是否应该归为该类了（如下图）

• 比如我们想将坐标上的所有数据点分为两类（如下图中）红色圈内希望预测为y=1；圈外希望预测为y=0。通过训练数据集呢，我们得到了一组θ值(θ0,θ1,θ2,θ3)=(-0.5,1,1,0)以及三个点(L1，L2，L3)，（具体怎么训练而成的大家先不要过分纠结，后面会讲）
• 对于每个test数据集中的点，我们首先计算它到（L1，L2，L3)各自的相似度，也就是核函数的值（f1，f2，f3），然后带入多项式θ₀f₀+θ₁f₁+…+θ_nf_n计算，当它>=0时，预测结果为类内点（正样本，y=1），else预测为负样本，y=0

=====================================

（五）、SVM 中 Gaussian Kernel 的使用

§5.1.    landmark的选取和参数向量θ的求解

上一节中我们遗留了两个问题，一个是一些L点的选取，一个是向量θ计算。这一节我们就来讲讲这两个问题。

首先来看L的选取。上一节中一提到Gaussian kernel fi 的计算：

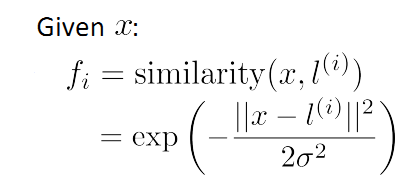
这里呢，我们选择m个训练数据，并取这m个训练数据为m个landmark（L）点（不考虑证样本还是负样本），如下图所示：

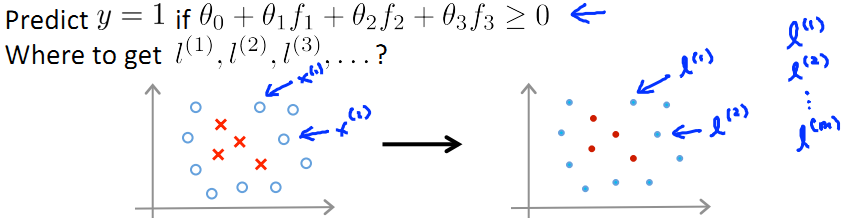
PS：那么在这m个训练数据中，每一个训练数据x(i)所得的特征向量（核函数）f中，总有一维向量的值为1（因为这里x(i)=l(i)）

于是，每个特征向量f有m+1维（m维训练数据[f1,f2,...,fm]附加一维f0=1）

在SVM的训练中，将Gaussian Kernel带入cost function,通过最小化该函数就可与得到参数θ，并根据该参数θ进行预测：

若θ^Tf>=0，predicty=1;

else predict y=0;

如下图所示，这里与之前讲过的cost function的区别在于用kernel f 代替了x。

§5.2.    landmark的选取和参数向量θ的求解

好了，至此Landmark点和θ的求取都解决了，还有一个问题，就是cost function中两个参数的确定：C和σ²。

对于C，由于C=1/λ，所以

C大，λ小，overfit，产生low bias，high variance

C小，λ大，underfit，产生high bias，low variance

详细原因请参考第六章中关于bias和variance的讲解。

对于方差σ²，和正态分布中的定义一样，

σ²大，x-f 图像较为扁平;

σ²小，x-f 图像较为窄尖;

关于C和σ²的选取，我们来做个练习：

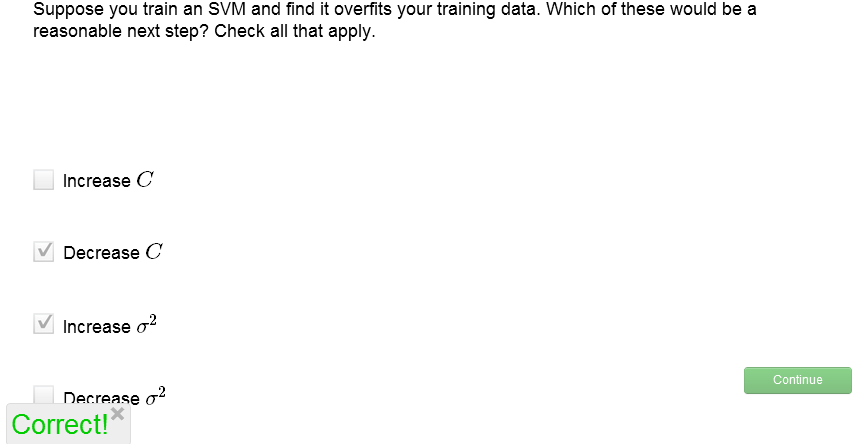
解析，过拟合说明应该适当加强cost function中的正则项所起的作用，因此应增大λ，即减小C；同时，过拟合是的只有一小部分范围内的x享有较大f，或者说x的覆盖面太窄了，所以应当增大σ²。

=====================================

（六）、SVM 的 使用与选择

本节中主要介绍SVM在matlab中用libsvm中的应用，给大家一个用SVM进行实践的平台。

前面几节中我们已知用SVM进行机器学习的过程就是一个optimize参数θ的过程，这里呢，我们首先介绍一个 Chih-Chung Chang 和 Chih-Jen Lin 做的 matlab/C/Ruby/Python/Java...中通用的机器学习tool，libsvm，其基本讲解和测试我以前讲过（在这里），算是入门篇，并不详细，这里呢，我们将结合本章课程近一步学习，并用matlab实现。

首先大家来看看，想要进行SVM学习，有哪两类：

一种是No kernel（linear kernel），h_θ(x)=g(θ₀x₀+θ₁x₁+…+θ_nx_{n)，predict y=1 if θ^Tx>=0;}

_{另一种是使用kernel f（比如Gaussian Kernel），hθ(x)=g(θ0f0+θ1f1+…+θnfn)，这里需要选择方差参数σ²}

如下图所示：

需要注意的是，不管用那种方法，都需要在ML之前进行Normalization归一化！

当然，除了Gaussian kernel,我们还有很多其他的kernel可以用，比如polynomial kernel等，如下图所示，但andrew表示他本人不会经常去用（或者几乎不用）以下"more esoteric"中的核，一个原因是其他的核不一定起作用。我们讲一下polynomial kernel:

polynomial 核形如 K（x，l）= (x^Tl+c)^d，也用来表示两个object的相似度

首先给大家引入一个数据集，在该数据集中，我们可以进行初步的libsvm训练和预测，如这篇文章中所说，这个也是最基本的no kernel(linear kernel)。

然后呢，给大家一个reference，这是libsvm中traing基本的语法：

该例中我们分别生成了100个正样本和100个负样本，如下图所示，因为kernel type default=2（即Gaussian kernel），通过svmtrain(datalabel，data，‘-c 100 -g 4‘)我们设置了第五节中奖的参数——C（c）和 2σ²（g）分别为100和4。

运行结果：

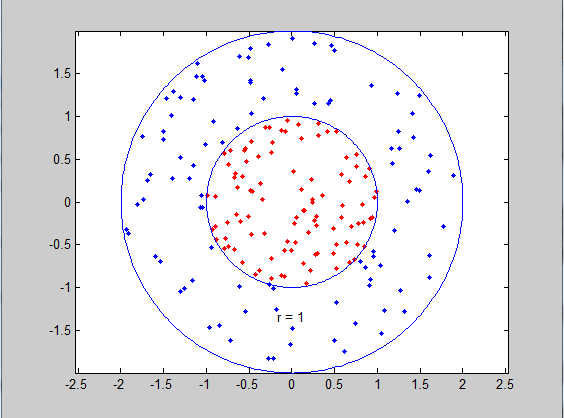
最后，我们比较一下logistic regresion和 SVM：

用n表示feature个数，m表示training exampl个数。

①当n>=m，如n=10000，m=10~1000时，建议用logistic regression, 或者linear kernel的SVM

②如果n小，m不大不小，如n=1~1000，m=10~10000，建议用Gaussian Kernel的SVM

③如果n很小，m很大，如n=1~1000，m>50000，建议增加更多的feature并使用logistic regression, 或者linear kernel的SVM

原因，①模型简单即可解决，③如果还用Gaussian kernel会导致很慢，所以还选择logistic regression或者linear kernel

神经网络可以解决以上任何问题，但是速度是一个很大的问题。

详见下图：

test：

我们可以把所有数据分为testset和training set两部分进行训练，example：

运行结果：

Reference:

1.How to build a custom Kernel function and use it with Libsvm in C?

2.Libsvm在matlab中的使用

3. SVM parameter tuning and number of SVs (Matlab libsvm)

4.Libsvm for matlab_Kittipat

Stanford机器学习---第八讲. 支持向量机SVM

标签：

原文地址：http://blog.csdn.net/liugallup/article/details/50993671