标签:
Farmer John wants to repair a small length of the fence around the pasture. He measures the fence and finds that he needs N (1 ≤ N ≤ 20,000) planks of wood, each having some integer length Li (1 ≤ Li≤ 50,000) units. He then purchases a single long board just long enough to saw into the N planks (i.e., whose length is the sum of the lengths Li). FJ is ignoring the "kerf", the extra length lost to sawdust when a sawcut is made; you should ignore it, too.
FJ sadly realizes that he doesn‘t own a saw with which to cut the wood, so he mosies over to Farmer Don‘s Farm with this long board and politely asks if he may borrow a saw.
Farmer Don, a closet capitalist, doesn‘t lend FJ a saw but instead offers to charge Farmer John for each of the N-1 cuts in the plank. The charge to cut a piece of wood is exactly equal to its length. Cutting a plank of length 21 costs 21 cents.
Farmer Don then lets Farmer John decide the order and locations to cut the plank. Help Farmer John determine the minimum amount of money he can spend to create the N planks. FJ knows that he can cut the board in various different orders which will result in different charges since the resulting intermediate planks are of different lengths.
3 8 5 8
34

#include <cstdio> #include <algorithm> #include <queue> #include <vector> using namespace std; typedef long long ll; struct cmp_min { bool operator() ( const int &a, const int &b ) { return a > b; } }; int main(void) { //freopen( "d://test.c", "rw+", stdin ); int n; ll t, ans; priority_queue < ll, vector < ll >, cmp_min > pri_que; while( scanf( "%d", &n ) != EOF ){ ans = 0; while( n -- ){ scanf( "%lld", &t ); pri_que.push( t ); } while( pri_que.size() != 1 ){ t = pri_que.top(); pri_que.pop(); t += pri_que.top(); pri_que.pop(); pri_que.push( t ); ans += t; } printf( "%lld\n", ans ); pri_que.pop(); } return 0; }
一、哈夫曼树的概念和定义
什么是哈夫曼树?
让我们先举一个例子。
判定树:

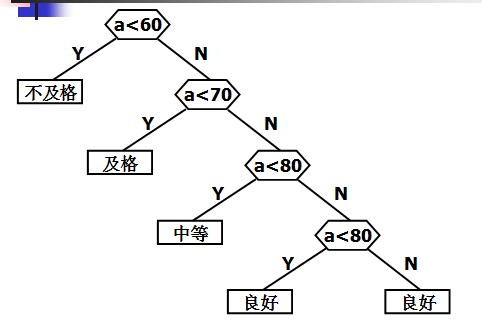
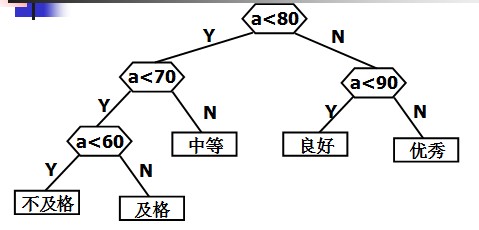
定义哈夫曼树之前先说明几个与哈夫曼树有关的概念:
路径: 树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
路径长度:路径上的分枝数目称作路径长度。
树的路径长度:从树根到每一个结点的路径长度之和。
结点的带权路径长度:在一棵树中,如果其结点上附带有一个权值,通常把该结点的路径长度与该结点上的权值
之积称为该结点的带权路径长度(weighted path length)
什么是权值?( From 百度百科 )
计算机领域中(数据结构)
权值就是定义的路径上面的值。可以这样理解为节点间的距离。通常指字符对应的二进制编码出现的概率。
至于霍夫曼树中的权值可以理解为:权值大表明出现概率大!
一个结点的权值实际上就是这个结点子树在整个树中所占的比例.
abcd四个叶子结点的权值为7,5,2,4. 这个7,5,2,4是根据实际情况得到的,比如说从一段文本中统计出abcd四个字母出现的次数分别为7,5,2,4. 说a结点的权值为7,意思是说a结点在系统中占有7这个份量.实际上也可以化为百分比来表示,但反而麻烦,实际上是一样的.
树的带权路径长度:如果树中每个叶子上都带有一个权值,则把树中所有叶子的带权路径长度之和称为树的带
权路径长度。
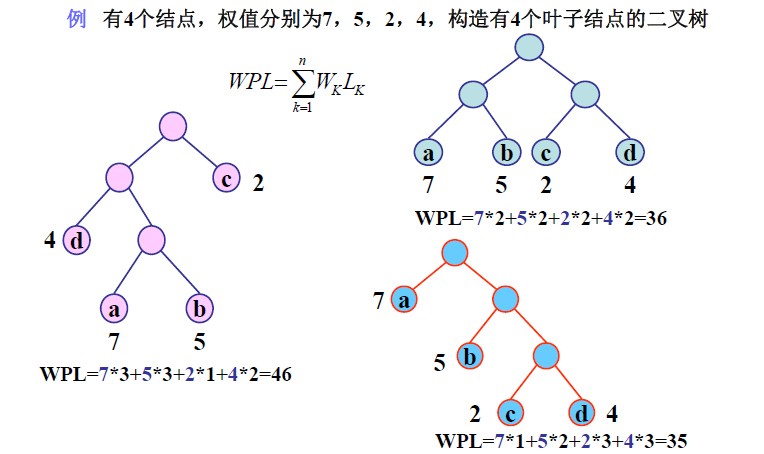
设某二叉树有n个带权值的叶子结点,则该二叉树的带权路径长度记为:

公式中,Wk为第k个叶子结点的权值;Lk为该结点的路径长度。
示例:
二、哈夫曼树的构造


三、哈夫曼树的在编码中的应用
标签:
原文地址:http://www.cnblogs.com/seana/p/5332446.html