标签:
一.树
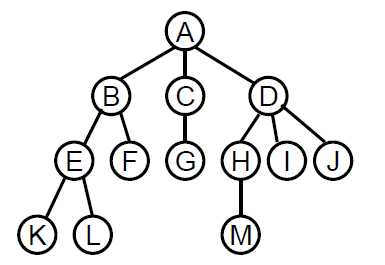
树的基本术语
①结点的度(Degree):结点的子树个数
②树的度:树的所有结点中最大的度数
③叶结点(Leaf):度为0的结点
④父结点(Parent):有子树的结点是其子树的根结点的父结点
⑤子结点(Child):若A结点是B结点的父结点,则称B结点是A结点的子结点;子结点也称孩子结点。
⑥兄弟结点(Sibling):具有同一父结点的各结点彼此是兄弟结点。
⑦路径和路径长度:从结点n1到nk的路径为一个结点序列n1 , n2 ,… , nk , ni是 ni+1的父结点。路径所包含边的个数为路径的长度。
⑧ 祖先结点(Ancestor):沿树根到某一结点路径上的所有结点都是这个结点的祖先结点。
⑨子孙结点(Descendant):某一结点的子树中的所有结点是这个结点的子孙。
⑩结点的层次(Level):规定根结点在1层,其它任一结点的层数是其父结点的层数加1。 12. 树的深度(Depth):树中所有结点中的最大层次是这棵树的深度。
二.二叉树
二叉树的性质
①一个二叉树第 i 层的最大结点数为:2^(i-1) (i>=1)
②深度为k的二叉树至多有2^k-1个结点 (i>=1)
③对任何非空二叉树 T,若n0表示叶结点的个数、n2是度为2的非叶结点个数,那么两者满足关系n0 = n2 +1 ---> n0+n1+n2 = B + 1 = n0 * 0 + n1 * 1 + n2 * 2
1.顺序存储结构
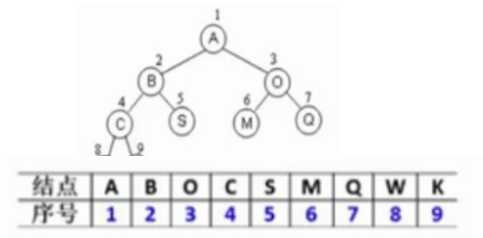
完全二叉树:按从上至下、从左到右顺序存储
N个结点的完全二叉树的结点父子关系:
① 非根结点(序号i > 1)的父结点的序号[ i / 2]
② 结点(序号为i) 的左孩子结点序号 2i,(若2i <=n,否则无左孩子)
③ 结点(序号为i) 的左孩子结点序号 2i +1,(若2i + 1<=n,否则无右孩子)
非完全二叉树 ---> 补全为完全二叉树
2.链式存储结构(代码:sj4_0)

1 //二叉树 2 #include <iostream> 3 #include <cstdio> 4 #include <stdlib.h> 5 #include <stack> 6 #include <queue> 7 using namespace std; 8 #define OK 1 9 #define ERROR 0 10 #define OVERFLOW -1 11 12 typedef int Status;/* Status是函数的类型,其值是函数结果状态代码,如OK等 */ 13 typedef int TElemType;/* ElemType类型根据实际情况而定,这里假设为int*/ 14 15 typedef struct BinTNode *BinTree; 16 struct BinTNode 17 { 18 TElemType data; 19 BinTree left; 20 BinTree right; 21 }; 22 23 Status CreatBiTree(BinTree &T); 24 Status PreOrderTraverse(BinTree T); 25 Status InOderTraverse(BinTree T); 26 Status PostOrderTraverse(BinTree T); 27 28 Status StackPreOrderTraverse(BinTree T); 29 Status StackInOrderTraverse(BinTree T); 30 Status StackPostOrderTraverse(BinTree T); 31 32 Status LevelOrderTraverse(BinTree T); 33 34 int PostOrderGetHeight(BinTree T); 35 36 Status InitBiTree(BinTree &T); 37 Status DestroyBiTree(BinTree &T); 38 Status ClearBiTree(BinTree &T); 39 bool BiTreeEmpty(BinTree T); 40 TElemType Root(BinTree T); 41 TElemType Value(BinTree p); 42 void Assign(BinTree p,TElemType value); 43 44 /*按先序次序输入二叉树中的结点值,负数表示空树 45 构造二叉链表表示的二叉树*/ 46 Status CreatBiTree(BinTree &T) 47 { 48 TElemType data; 49 scanf("%d",&data); 50 if(data < 0 ) 51 T = NULL; 52 else { 53 if( !(T = (BinTree)malloc(sizeof(BinTNode))) ) 54 exit(OVERFLOW); 55 T->data = data; 56 CreatBiTree(T->left); 57 CreatBiTree(T->right); 58 } 59 return OK; 60 } 61 62 //递归实现先序遍历 63 Status PreOrderTraverse(BinTree T) 64 { 65 if(T) { 66 printf("%5d", T->data); 67 PreOrderTraverse(T->left); 68 PreOrderTraverse(T->right); 69 } 70 return OK; 71 } 72 //递归实现中序遍历 73 Status InOderTraverse(BinTree T) 74 { 75 if(T) { 76 PreOrderTraverse(T->left); 77 printf("%5d", T->data); 78 PreOrderTraverse(T->right); 79 } 80 return OK; 81 } 82 //递归实现后序遍历 83 Status PostOrderTraverse(BinTree T) 84 { 85 if(T) { 86 PreOrderTraverse(T->left); 87 PreOrderTraverse(T->right); 88 printf("%5d", T->data); 89 } 90 return OK; 91 } 92 93 //非递归实现先序遍历:堆栈 94 Status StackPreOrderTraverse(BinTree T) 95 { 96 if(T == NULL) 97 return ERROR; 98 BinTree BT = T; 99 stack<BinTree> stack; 100 while(BT || !stack.empty() ) { 101 while(BT) { //一直向左将沿途结点压入堆栈 102 printf("%5d",BT->data); //访问打印结点 103 stack.push(BT); 104 BT = BT->left; 105 } 106 if( !stack.empty() ) { 107 BT = stack.top(); //记录弹出结点 108 stack.pop(); 109 BT = BT->right; //转向右子树 110 } 111 } 112 return OK; 113 } 114 115 //非递归实现中序遍历:堆栈 116 Status StackInOrderTraverse(BinTree T) 117 { 118 if(T == NULL) 119 return ERROR; 120 BinTree BT = T; 121 stack<BinTree> stack; 122 while(BT || !stack.empty() ) { 123 while(BT) { //一直向左将沿途结点压入堆栈 124 stack.push(BT); 125 BT = BT->left; 126 } 127 if( !stack.empty() ) { ////// 128 BT = stack.top(); //记录弹出结点 129 stack.pop(); 130 printf("%5d",BT->data); //访问打印结点 131 BT = BT->right; //转向右子树 132 } 133 } 134 return OK; 135 } 136 137 //非递归实现后序遍历:堆栈 138 /*后序遍历LRG:第一遍入栈,G再第二遍被遍历到时,若有右孩子,则入栈(等待第三次遍历); 139 如无右孩子,或右孩子已被访问,则访问G结点。*/ 140 Status StackPostOrderTraverse(BinTree T) 141 { 142 if(T == NULL) 143 return ERROR; 144 BinTree BT = T; 145 stack<BinTree> stack; 146 BinTree lastNode = NULL, currentNode = NULL;//lastNode记录被访问过的前一个结点 147 while( BT || !stack.empty() ) { 148 while(BT) { //一直向左将沿途结点压入堆栈 149 stack.push(BT); 150 BT = BT->left; 151 } 152 while( !stack.empty() ) { 153 currentNode = stack.top(); //当前节点 154 stack.pop(); //出栈 155 if( currentNode->right == NULL || currentNode->right == lastNode) {//无右子树或右子树已被访问 156 printf("%5d",currentNode->data); 157 lastNode = currentNode; 158 }else { //右子树未被访问过 159 stack.push(currentNode); 160 currentNode = currentNode->right; 161 while(currentNode) { 162 stack.push(currentNode); 163 currentNode = currentNode->left; 164 } 165 } 166 } 167 } 168 return OK; 169 } 170 171 //层序遍历:队列 172 Status LevelOrderTraverse(BinTree T) 173 { 174 if(T == NULL) 175 return ERROR; 176 BinTree BT = T; 177 queue<BinTree> queue; 178 queue.push(BT); 179 while( !queue.empty() ) { 180 BinTree temp = queue.front(); 181 printf("%5d", temp->data); 182 queue.pop(); 183 if(temp->left) 184 queue.push(temp->left); 185 if(temp->right) 186 queue.push(temp->right); 187 } 188 printf("\n"); 189 return OK; 190 } 191 192 //后序遍历求树深度(高) 193 int PostOrderGetHeight(BinTree T) 194 { 195 int leftHeight, rightHeight, maxHeight; 196 if(T) { 197 leftHeight = PostOrderGetHeight(T->left); //左子树深度 198 rightHeight = PostOrderGetHeight(T->right); //右子树深度 199 maxHeight = leftHeight > rightHeight ? leftHeight : rightHeight; 200 return (maxHeight+1); //返回树的深度 201 } 202 else 203 return 0;//空树深度为0 204 } 205 206 //构造空二叉树T 207 Status InitBiTree(BinTree &T) 208 { 209 T = NULL; 210 return OK; 211 } 212 //销毁二叉树T 213 Status DestroyBiTree(BinTree &T) 214 { 215 if(T) { 216 if(T->left) 217 DestroyBiTree(T->left); 218 if(T->right) 219 DestroyBiTree(T->right); 220 free(T); //释放该结点 221 T = NULL; //T置空 222 } 223 return OK; 224 } 225 /*清空二叉树T 226 清空和销毁有什么区别么*/ 227 Status ClearBiTree(BinTree &T) 228 { 229 if(T) { 230 if(T->left) 231 DestroyBiTree(T->left); 232 if(T->right) 233 DestroyBiTree(T->right); 234 free(T); //释放该结点 235 T = NULL; //T置空 236 } 237 return OK; 238 } 239 240 bool BiTreeEmpty(BinTree T) 241 { 242 if( !T ) 243 return true; 244 else 245 return false; 246 } 247 248 //返回T的根 249 TElemType Root(BinTree T) 250 { 251 if(BiTreeEmpty(T)) 252 return -1; 253 else 254 return T->data; 255 } 256 257 //返回p所指结点的值 258 TElemType Value(BinTree p) 259 { 260 return p->data; 261 } 262 263 // 给p所指结点赋值为value 264 void Assign(BinTree p,TElemType value) 265 { 266 p->data=value; 267 } 268 269 270 271 int main() 272 { 273 BinTree T; 274 CreatBiTree(T); 275 printf("先序递归遍历: "); 276 PreOrderTraverse(T); 277 printf("\n先序非递归遍历:"); 278 StackPreOrderTraverse(T); 279 280 printf("\n中序递归遍历: "); 281 InOderTraverse(T); 282 printf("\n中序非递归遍历:"); 283 StackInOrderTraverse(T); 284 285 printf("\n后序递归遍历: "); 286 PostOrderTraverse(T); 287 printf("\n后序非递归遍历:"); 288 StackPostOrderTraverse(T); 289 290 printf("\n层序遍历: "); 291 LevelOrderTraverse(T); 292 printf("\n树的高度:%d\n",PostOrderGetHeight(T)); 293 if(BiTreeEmpty(T)) 294 printf("空\n"); 295 else 296 printf("不空\n"); 297 printf("树的根:%d\n",Root(T)); 298 299 300 301 return 0; 302 }
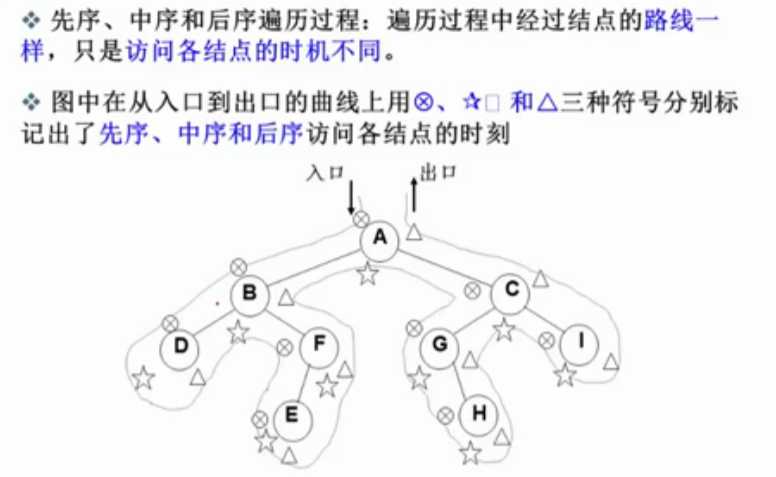
先序GLR:第一次遇到该结点则输出。
中序LGR:第二次遇到该结点则输出。
后序LRG:第三次遇到该结点则输出。
typedef struct BinTNode *BinTree;
struct BinTNode
{
TElemType data;
BinTree left;
BinTree right;
};
先序递归算法

1 //递归实现先序遍历 2 Status PreOrderTraverse(BinTree T) 3 { 4 if(T) { 5 printf("%5d", T->data); 6 PreOrderTraverse(T->left); 7 PreOrderTraverse(T->right); 8 } 9 return OK; 10 }
先序遍历非递归遍历算法
①遇到一个结点,访问打印它,将其压栈,并遍历它的左子树
②当左子树遍历结束后,从栈顶弹出这个结点
③然后按其右指针再去先序遍历该结点的右子树

1 Status StackPreOrderTraverse(BinTree T) 2 { 3 if(T == NULL) 4 return ERROR; 5 BinTree BT = T; 6 stack<BinTree> stack; 7 while(BT || !stack.empty() ) { 8 while(BT) { //一直向左将沿途结点压入堆栈 9 printf("%5d",BT->data); //访问打印结点 10 stack.push(BT); 11 BT = BT->left; 12 } 13 if( !stack.empty() ) { 14 BT = stack.top(); //记录弹出结点 15 stack.pop(); 16 BT = BT->right; //转向右子树 17 } 18 } 19 return OK; 20 }
中序遍历非递归遍历算法
①遇到一个结点,就把它压栈,并遍历它的左子树
②当左子树遍历结束后,从栈顶弹出这个结点并访问它
③然后按其右指针再去中序遍历该结点的右子树

1 //非递归实现中序遍历:堆栈 2 Status StackInOrderTraverse(BinTree T) 3 { 4 if(T == NULL) 5 return ERROR; 6 BinTree BT = T; 7 stack<BinTree> stack; 8 while(BT || !stack.empty() ) { 9 while(BT) { //一直向左将沿途结点压入堆栈 10 stack.push(BT); 11 BT = BT->left; 12 } 13 if( !stack.empty() ) { ////// 14 BT = stack.top(); //记录弹出结点 15 stack.pop(); 16 printf("%5d",BT->data); //访问打印结点 17 BT = BT->right; //转向右子树 18 } 19 } 20 return OK; 21 }
后序遍历非递归算法
后序遍历LRG:第一遍入栈,G再第二遍被遍历到时,若有右孩子,则入栈(等待第三次遍历);如无右孩子,或右孩子已被访问,则访问G结点。

1 //非递归实现后序遍历:堆栈 2 Status StackPostOrderTraverse(BinTree T) 3 { 4 if(T == NULL) 5 return ERROR; 6 BinTree BT = T; 7 stack<BinTree> stack; 8 BinTree lastNode = NULL, currentNode = NULL;//lastNode记录被访问过的前一个结点 9 while( BT || !stack.empty() ) { 10 while(BT) { //一直向左将沿途结点压入堆栈 11 stack.push(BT); 12 BT = BT->left; 13 } 14 while( !stack.empty() ) { 15 currentNode = stack.top(); //当前节点 16 stack.pop(); //出栈 17 if( currentNode->right == NULL || currentNode->right == lastNode) {//无右子树或右子树已被访问 18 printf("%5d",currentNode->data); 19 lastNode = currentNode; 20 }else { //右子树未被访问过 21 stack.push(currentNode); 22 currentNode = currentNode->right; 23 while(currentNode) { 24 stack.push(currentNode); 25 currentNode = currentNode->left; 26 } 27 } 28 } 29 } 30 return OK; 31 }
层序遍历算法:先根结点入队,然后
①从队列取出一个元素
②访问打印该元素所指结点
③若该元素有左右孩子,则左右孩子顺序入队

1 //层序遍历:队列 2 Status LevelOrderTraverse(BinTree T) 3 { 4 if(T == NULL) 5 return ERROR; 6 BinTree BT = T; 7 queue<BinTree> queue; 8 queue.push(BT); 9 while( !queue.empty() ) { 10 BinTree temp = queue.front(); 11 printf("%5d", temp->data); 12 queue.pop(); 13 if(temp->left) 14 queue.push(temp->left); 15 if(temp->right) 16 queue.push(temp->right); 17 } 18 printf("\n"); 19 return OK; 20 }
三.二叉搜索树(二叉排序树 二叉查找树)(代码:sj4_1)

1 //二叉搜索树(BST) 2 #include <stdio.h> 3 #include <stdlib.h> 4 5 #define OK 1 6 #define ERROR 0 7 #define OVERFLOW -1 8 9 typedef int Status;/* Status是函数的类型,其值是函数结果状态代码,如OK等 */ 10 typedef int TElemType;/* ElemType类型根据实际情况而定,这里假设为int*/ 11 12 13 typedef struct BinTNode *BSTree; 14 struct BinTNode 15 { 16 TElemType data; 17 BSTree left; 18 BSTree right; 19 }; 20 //查找X,若成功返回结点地址,失败返回NULL 21 BSTree Find(TElemType X,BSTree BST) 22 { 23 while(BST) { 24 if(X < BST->data) 25 BST = BST->left; 26 else if(X > BST->data) 27 BST = BST->right; 28 else 29 return BST; 30 } 31 return NULL; 32 } 33 //从二叉搜索树BST中查找并返回最小元素所在结点的地址 34 BSTree FindMin(BSTree BST) 35 { 36 if(BST) 37 while(BST->left) 38 BST = BST->left; 39 return BST; 40 } 41 42 //从二叉搜索树BST中查找并返回最大元素所在结点的地址 43 BSTree FindMax(BSTree BST) 44 { 45 if(BST) 46 while(BST->right) 47 BST = BST->right; 48 return BST; 49 } 50 51 //插入结点X 52 BSTree Insert(TElemType X,BSTree BST) 53 { 54 if(!BST) { //空则建结点 55 BST = (BSTree)malloc(sizeof(struct BinTNode)); 56 BST->data = X; 57 BST->left = BST->right = NULL; 58 }else { 59 if(X > BST->data) //X大于该结点,递归插入右子树 60 Insert(X,BST->right); 61 else if(X < BST->data) //X小于该结点,递归插入做子树 62 Insert(X,BST->left); 63 //相等,已存在,什么都不做 64 } 65 return BST; 66 } 67 68 //删除结点X 69 BSTree Delete(TElemType X,BSTree BST) 70 { 71 if(!BST) { 72 printf("未找到要删除的结点\n"); 73 return ERROR; 74 } 75 if(X > BST->data) 76 BST->right = Delete(X,BST->right); 77 else if(X < BST->data) 78 BST->left = Delete(X,BST->left); 79 else { //找到要删除的结点 80 if(BST->left && BST->right) { //要删除结点有左右两个孩子 81 BSTree Temp = FindMin(BST); //在右子树中找到最小元素填充要删除元素 82 BST->data = Temp->data; 83 BST->right = Delete(Temp->data,BST->right);//删除最小元素 84 }else { //要删除结点只有一个孩子或没有孩子 85 BSTree Temp = BST; 86 if(!BST->left) //如果左孩子空 87 BST = BST->right; 88 if(!BST->right) //如果右孩子空 89 BST = BST->left; 90 free(Temp); 91 } 92 } 93 return BST; 94 }
二叉搜索树:一棵二叉树,可以为空;如果不为空,满足以下性质:
①非空左子树的所有键值小于其根结点的键值。
② 非空右子树的所有键值大于其根结点的键值。
③ 左、右子树都是二叉搜索树。
BSTree Find(TElemType X,BSTree BST):从二叉搜索树BST中查找元素X,返回其所在结点的地址;
BSTree FindMin(BSTree BST)从二叉搜索树BST中查找并返回最小元素所在结点的地址;
BSTree FindMax(BSTree BST):从二叉搜索树BST中查找并返回最大元素所在结点的地址。
BSTree Insert(TElemType X,BSTree BST)
BSTree Delete(TElemType X,BSTree BST)
1.二叉搜索树的查找
算法思路:查找从根结点开始,如果树为空,返回NULL
若搜索树非空,则根结点关键字和X进行比较,并进行不同处理:
若X小于根结点键值,只需在左子树中继续搜索;
如果X大于根结点的键值,在右子树中进行继续搜索;
若两者比较结果是相等,搜索完成,返回指向此结点的指针。
最大元素一定是在树的最右分枝的端结点上
最小元素一定是在树的最左分枝的端结点上

1 //查找X,若成功返回结点地址,失败返回NULL 2 BSTree Find(TElemType X,BSTree BST) 3 { 4 while(BST) { 5 if(X < BST->data) 6 BST = BST->left; 7 else if(X > BST->data) 8 BST = BST->right; 9 else 10 return BST; 11 } 12 return NULL; 13 } 14 //从二叉搜索树BST中查找并返回最小元素所在结点的地址 15 BSTree FindMin(BSTree BST) 16 { 17 if(BST) 18 while(BST->left) 19 BST = BST->left; 20 return BST; 21 } 22 23 //从二叉搜索树BST中查找并返回最大元素所在结点的地址 24 BSTree FindMax(BSTree BST) 25 { 26 if(BST) 27 while(BST->right) 28 BST = BST->right; 29 return BST; 30 }
2.二叉搜索树的删除
三种情况:
①要删除的是叶结点:直接删除,并再修改其父结点指针---置为NULL
②要删除的结点只有一个孩子结点: 将其父结点的指针指向要删除结点的孩子结点
③要删除的结点有左、右两棵子树: 用另一结点替代被删除结点:右子树的最小元素 或者 左子树的最大元素

1 //删除结点X 2 BSTree Delete(TElemType X,BSTree BST) 3 { 4 if(!BST) { 5 printf("未找到要删除的结点\n"); 6 return ERROR; 7 } 8 if(X > BST->data) 9 BST->right = Delete(X,BST->right); 10 else if(X < BST->data) 11 BST->left = Delete(X,BST->left); 12 else { //找到要删除的结点 13 if(BST->left && BST->right) { //要删除结点有左右两个孩子 14 BSTree Temp = FindMin(BST); //在右子树中找到最小元素填充要删除元素 15 BST->data = Temp->data; 16 BST->right = Delete(Temp->data,BST->right);//删除最小元素 17 }else { //要删除结点只有一个孩子或没有孩子 18 BSTree Temp = BST; 19 if(!BST->left) //如果左孩子空 20 BST = BST->right; 21 if(!BST->right) //如果右孩子空 22 BST = BST->left; 23 free(Temp); 24 } 25 } 26 return BST; 27 }
四.平衡二叉树(Balanced Binary Tree)(AVL树)(代码:sj4_2)

1 //平衡二叉树 AVL 2 #include <stdio.h> 3 #include <stdlib.h> 4 5 typedef int ElementType; 6 7 typedef struct AVLNode *Position; 8 typedef Position AVLTree; /* AVL树类型 */ 9 typedef struct AVLNode{ 10 ElementType data; /* 结点数据 */ 11 AVLTree left; /* 指向左子树 */ 12 AVLTree right; /* 指向右子树 */ 13 int height; /* 树高 */ 14 }; 15 16 int Max ( int a, int b ) 17 { 18 return a > b ? a : b; 19 } 20 21 int GetHeight( Position p ) 22 { 23 if(!p) 24 return -1; 25 return p->height; 26 } 27 28 /* 将A与B做左单旋,更新A与B的高度,返回新的根结点B */ 29 /* 注意:A必须有一个左子结点B */ 30 AVLTree SingleLeftRotation ( AVLTree A ) 31 { 32 AVLTree B = A->left; 33 A->left = B->right; 34 B->right = A; 35 A->height = Max( GetHeight(A->left), GetHeight(A->right) ) + 1; 36 B->height = Max( GetHeight(B->left), A->height ) + 1; 37 38 return B; 39 } 40 /* 将A与B做右单旋,更新A与B的高度,返回新的根结点B */ 41 /* 注意:A必须有一个右子结点B */ 42 AVLTree SingleRightRotation ( AVLTree A ) 43 { 44 AVLTree B = A->right; 45 A->right = B->left; 46 B->left = A; 47 A->height = Max( GetHeight(A->left), GetHeight(A->right) ) + 1; 48 B->height = Max( A->height, GetHeight(B->right) ) + 1; 49 50 return B; 51 } 52 53 /* 注意:A必须有一个左子结点B,且B必须有一个右子结点C */ 54 /* 将A、B与C做两次单旋,返回新的根结点C */ 55 AVLTree DoubleLeftRightRotation ( AVLTree A ) 56 { 57 /* 将B与C做右单旋,C被返回 */ 58 A->left = SingleRightRotation(A->left); 59 /* 将A与C做左单旋,C被返回 */ 60 return SingleLeftRotation(A); 61 } 62 63 /* 将A、B与C做两次单旋,返回新的根结点C */ 64 /* 注意:A必须有一个右子结点B,且B必须有一个左子结点C */ 65 AVLTree DoubleRightLeftRotation ( AVLTree A ) 66 { 67 /* 将B与C做右单旋,C被返回 */ 68 A->right = SingleLeftRotation(A->right); 69 /* 将A与C做左单旋,C被返回 */ 70 return SingleRightRotation(A); 71 } 72 73 /* 将X插入AVL树T中,并且返回调整后的AVL树 */ 74 AVLTree Insert( AVLTree T, ElementType X ) 75 { 76 if ( !T ) { /* 若插入空树,则新建包含一个结点的树 */ 77 T = (AVLTree)malloc(sizeof(struct AVLNode)); 78 T->data = X; 79 T->height = 0; 80 T->left = T->right = NULL; 81 } /* if (插入空树) 结束 */ 82 83 else if ( X < T->data ) { 84 T->left = Insert( T->left, X);/* 插入T的左子树 */ 85 if ( GetHeight(T->left)-GetHeight(T->right) == 2 ) /* 如果需要左旋 */ 86 if ( X < T->left->data ) 87 T = SingleLeftRotation(T); //左单旋 LL 88 else 89 T = DoubleLeftRightRotation(T); //左-右双旋LR 90 } /* else if (插入左子树) 结束 */ 91 92 else if ( X > T->data ) { 93 T->right = Insert( T->right, X );/* 插入T的右子树 */ 94 if ( GetHeight(T->left)-GetHeight(T->right) == -2 )/* 如果需要右旋 */ 95 if ( X > T->right->data ) 96 T = SingleRightRotation(T); //右单旋 RR 97 else 98 T = DoubleRightLeftRotation(T); //右-左双旋 RL 99 } /* else if (插入右子树) 结束 */ 100 101 /*else X == T->Data,无须插入 */ 102 T->height = Max( GetHeight(T->left), GetHeight(T->right) ) + 1; //更新树高 103 104 return T; 105 } 106 107 int main() 108 { 109 int N, data; 110 AVLTree T; 111 scanf("%d",&N); 112 for(int i = 0; i < N; i++) { 113 scanf("%d",&data); 114 T = Insert(T,data); 115 } 116 printf("%d\n",T->data); 117 return 0; 118 }
平衡因子(Balance Factor,简称BF): BF(T) = hL-hR,
平衡二叉树:空树,或者 任一结点左、右子树高度差的绝对值不超过1,即|BF(T) |≤ 1
1.LL
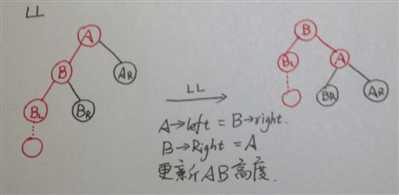

1 /* 将A与B做左单旋,更新A与B的高度,返回新的根结点B */ 2 /* 注意:A必须有一个左子结点B */ 3 AVLTree SingleLeftRotation ( AVLTree A ) 4 { 5 AVLTree B = A->left; 6 A->left = B->right; 7 B->right = A; 8 A->height = Max( GetHeight(A->left), GetHeight(A->right) ) + 1; 9 B->height = Max( GetHeight(B->left), A->height ) + 1; 10 11 return B; 12 }
2.RR
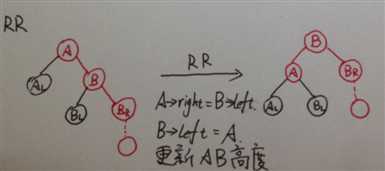

1 /* 将A与B做右单旋,更新A与B的高度,返回新的根结点B */ 2 /* 注意:A必须有一个右子结点B */ 3 AVLTree SingleRightRotation ( AVLTree A ) 4 { 5 AVLTree B = A->right; 6 A->right = B->left; 7 B->left = A; 8 A->height = Max( GetHeight(A->left), GetHeight(A->right) ) + 1; 9 B->height = Max( A->height, GetHeight(B->right) ) + 1; 10 11 return B; 12 }
3.LR
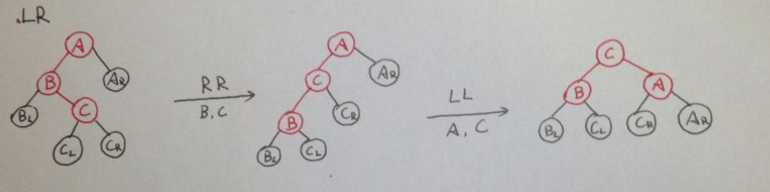

1 /* 注意:A必须有一个左子结点B,且B必须有一个右子结点C */ 2 /* 将A、B与C做两次单旋,返回新的根结点C */ 3 AVLTree DoubleLeftRightRotation ( AVLTree A ) 4 { 5 /* 将B与C做右单旋,C被返回 */ 6 A->left = SingleRightRotation(A->left); 7 /* 将A与C做左单旋,C被返回 */ 8 return SingleLeftRotation(A); 9 }
4.RL
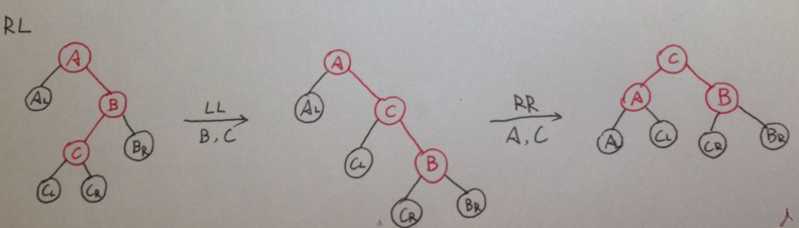

1 /* 将A、B与C做两次单旋,返回新的根结点C */ 2 /* 注意:A必须有一个右子结点B,且B必须有一个左子结点C */ 3 AVLTree DoubleRightLeftRotation ( AVLTree A ) 4 { 5 /* 将B与C做右单旋,C被返回 */ 6 A->right = SingleLeftRotation(A->right); 7 /* 将A与C做左单旋,C被返回 */ 8 return SingleRightRotation(A); 9 }
5.insert

1 /* 将X插入AVL树T中,并且返回调整后的AVL树 */ 2 AVLTree Insert( AVLTree T, ElementType X ) 3 { 4 if ( !T ) { /* 若插入空树,则新建包含一个结点的树 */ 5 T = (AVLTree)malloc(sizeof(struct AVLNode)); 6 T->data = X; 7 T->height = 0; 8 T->left = T->right = NULL; 9 } /* if (插入空树) 结束 */ 10 11 else if ( X < T->data ) { 12 T->left = Insert( T->left, X);/* 插入T的左子树 */ 13 if ( GetHeight(T->left)-GetHeight(T->right) == 2 ) /* 如果需要左旋 */ 14 if ( X < T->left->data ) 15 T = SingleLeftRotation(T); //左单旋 LL 16 else 17 T = DoubleLeftRightRotation(T); //左-右双旋LR 18 } /* else if (插入左子树) 结束 */ 19 20 else if ( X > T->data ) { 21 T->right = Insert( T->right, X );/* 插入T的右子树 */ 22 if ( GetHeight(T->left)-GetHeight(T->right) == -2 )/* 如果需要右旋 */ 23 if ( X > T->right->data ) 24 T = SingleRightRotation(T); //右单旋 RR 25 else 26 T = DoubleRightLeftRotation(T); //右-左双旋 RL 27 } /* else if (插入右子树) 结束 */ 28 29 /*else X == T->Data,无须插入 */ 30 T->height = Max( GetHeight(T->left), GetHeight(T->right) ) + 1; //更新树高 31 32 return T; 33 }
标签:
原文地址:http://www.cnblogs.com/kuotian/p/5333956.html