软件测试homework3

标签：

一、对一个方法进行测试

private static  void printPrimes(int n){
        int curPrime;
        int numPrimes;
        boolean isPrime;
        int [] primes = new int [43];
        primes[0]=2;
        numPrimes = 1;
        curPrime = 2;
        while ( numPrimes < n)
        {
            curPrime ++ ;
            isPrime = true;
            for ( int i = 0 ; i <= numPrimes-1 ;i++){
                if (isDivisible(primes[i],curPrime))
                {
                    isPrime = false;
                    break ;
                }
            }
            if (isPrime){
                primes[numPrimes] = curPrime ;
                numPrimes ++ ;
                
            }
        }
        
        for (int i = 0 ; i <= numPrimes -1 ; i++ )
        {
            System.out.println("Prime: " + primes[i]);
        }
        
    }

1）画出此方法的控制流图

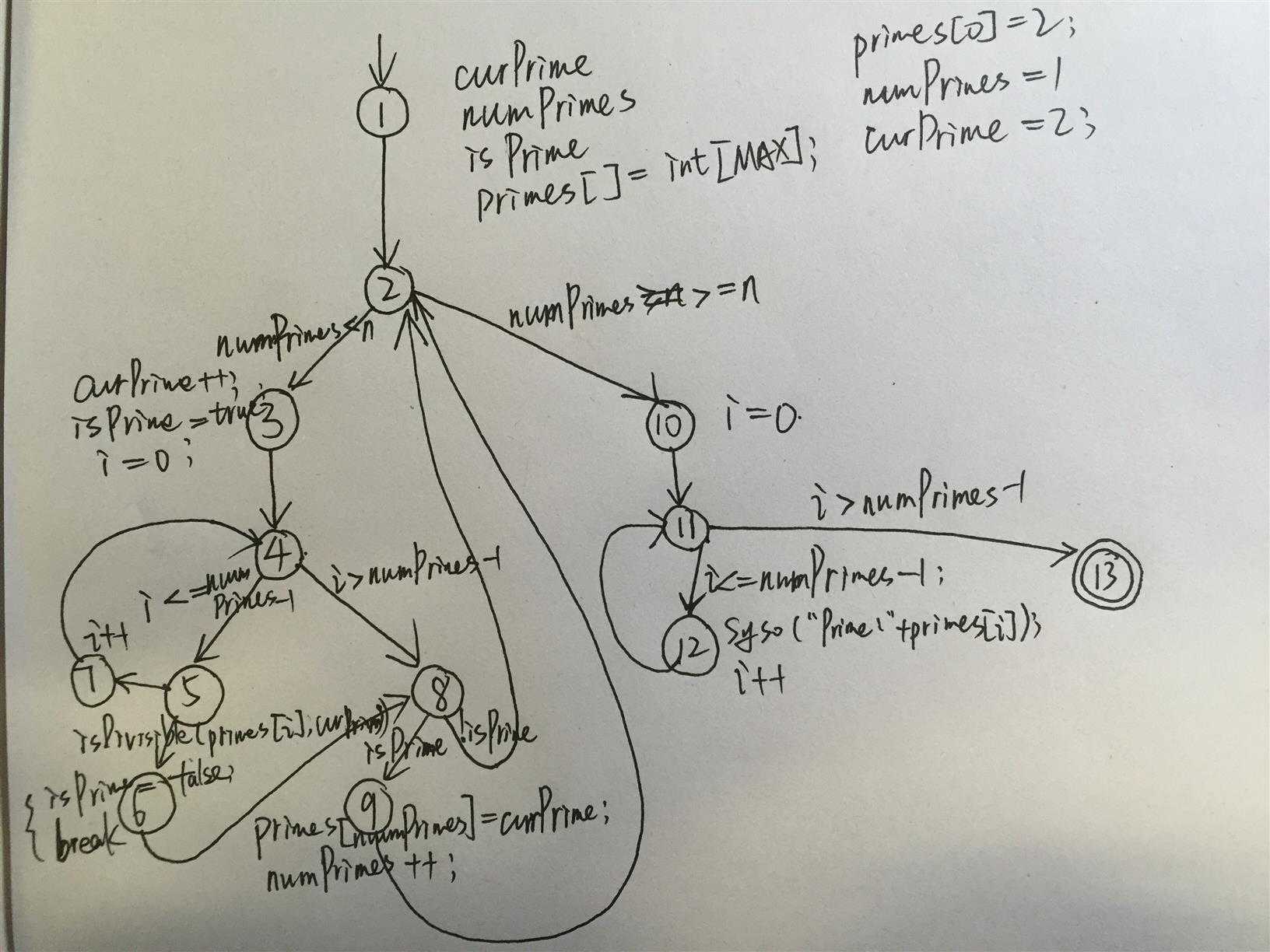
2）T1 ： n = 3 ;T2 : n = 5;

设计一个 Fault 使T2 能发现，T1不能发现：

答：

将  if ( isDivisible(primes[i],curPrime) 修改 为  if ( isDivisible(primes[0],curPrime) 

3）设计一个测试用例不经过While的body

答：

n <= 1 即可

4）枚举TR 对于 NC ,EC ，PPC 

TR :

i)NC:{1,2,3,4,5,6,7,8,9,10,11,12,13}

ii)EC:{(1,2),(2,3),(2,10),(3,4),(4,5),(4,8),(5,6),(5,7),(6,8),(7,4),(8,2),(8,9),

(9,2),(10,11),(11,12),(11,13),(12,11)}

iii)PPC:一共51条

A.[11,12,11] , [12,11,12]点11，12组成的环可以写出2条路径

B.点4，5，7 组成的环可以写出3条路径

C.点2，3，4，8组成的环可以写出4条路径

D.点2，3，4，8，9组成的环可以写出5条路径

E.点2，3，4，5，6，8组成的环可以写出6条路径

F.点2，3，4，5，6，8，9组成的环可以写出7条路径

G.点1出发的有5条：[1,2,10,11,13],[1,2,10,11,12],[1,2,3,4,5,7],[1,2,3,4,8,9],[1,2,3,4,5,6,8,9]

H.点3出发的有9条：[3,4,5,7],[3,4,8,2,10,11,12],[3,4,8,2,10,11,13],[3,4,8,9,2,10,11,12],[3,4,8,9,2,10,11,13],

[3,4,5,6,8,2,10,11,12],[3,4,5,6,8,2,10,11,13],[3,4,5,6,8,9,2,10,11,12],[3,4,5,6,8,9,2,10,11,13]

I.点5出发的有4条：[5,7,4,8,2,10,11,12],[5,7,4,8,2,10,11,13],[5,7,4,8,9,2,10,11,12],[5,7,4,8,9,2,10,11,13]

J.点7出发的有4条：[7,4,5,6,8,2,10,11,12],[7,4,5,6,8,2,10,11,13],[7,4,5,6,8,9,2,10,11,12],[7,4,5,6,8,9,2,10,11,13]

K.点8出发的有2条：[8,2,3,4,5,7],[8,2,3,4,5,6]

软件测试homework3

标签：

原文地址：http://www.cnblogs.com/tzy3013218117/p/5335533.html