标签:
程序代码如下:
1 /******************************************************* 2 * Finds and prints n prime integers 3 * Jeff Offutt, Spring 2003 4 ******************************************************/ 5 public static void printPrimes (int n) 6 { 7 int curPrime; // Value currently considered for primeness 8 int numPrimes; // Number of primes found so far. 9 boolean isPrime; // Is curPrime prime? 10 int [] primes = new int [MAXPRIMES]; // The list of prime numbers. 11 12 // Initialize 2 into the list of primes. 13 primes [0] = 2; 14 numPrimes = 1; 15 curPrime = 2; 16 while (numPrimes < n) 17 { 18 curPrime++; // next number to consider ... 19 isPrime = true; 20 for (int i = 0; i <= numPrimes-1; i++) 21 { // for each previous prime. 22 if (curPrime%primes[i]==0) 23 { // Found a divisor, curPrime is not prime. 24 isPrime = false; 25 break; // out of loop through primes. 26 } 27 } 28 if (isPrime) 29 { // save it! 30 primes[numPrimes] = curPrime; 31 numPrimes++; 32 } 33 } // End while 34 35 // Print all the primes out. 36 for (int i = 0; i <= numPrimes-1; i++) 37 { 38 System.out.println ("Prime: " + primes[i]); 39 } 40 } // end printPrimes
题目要求如下:
(a)Draw the control flow graph
(b)t1=(n=3),t2=(n=5) Design a simple fault that t2 would be more likely to discover than t1 would.
(c)Find a test case that connects the beginning of the while statement to for statement without going through the body of while loop.
(d)Enumerate the test requirements for node coverage, edge coverage, and prime path coverage.
– 基于Junit及Eclemma( jacoco)实现一个主路径覆盖的测试。
Solutions:
a)控制流图
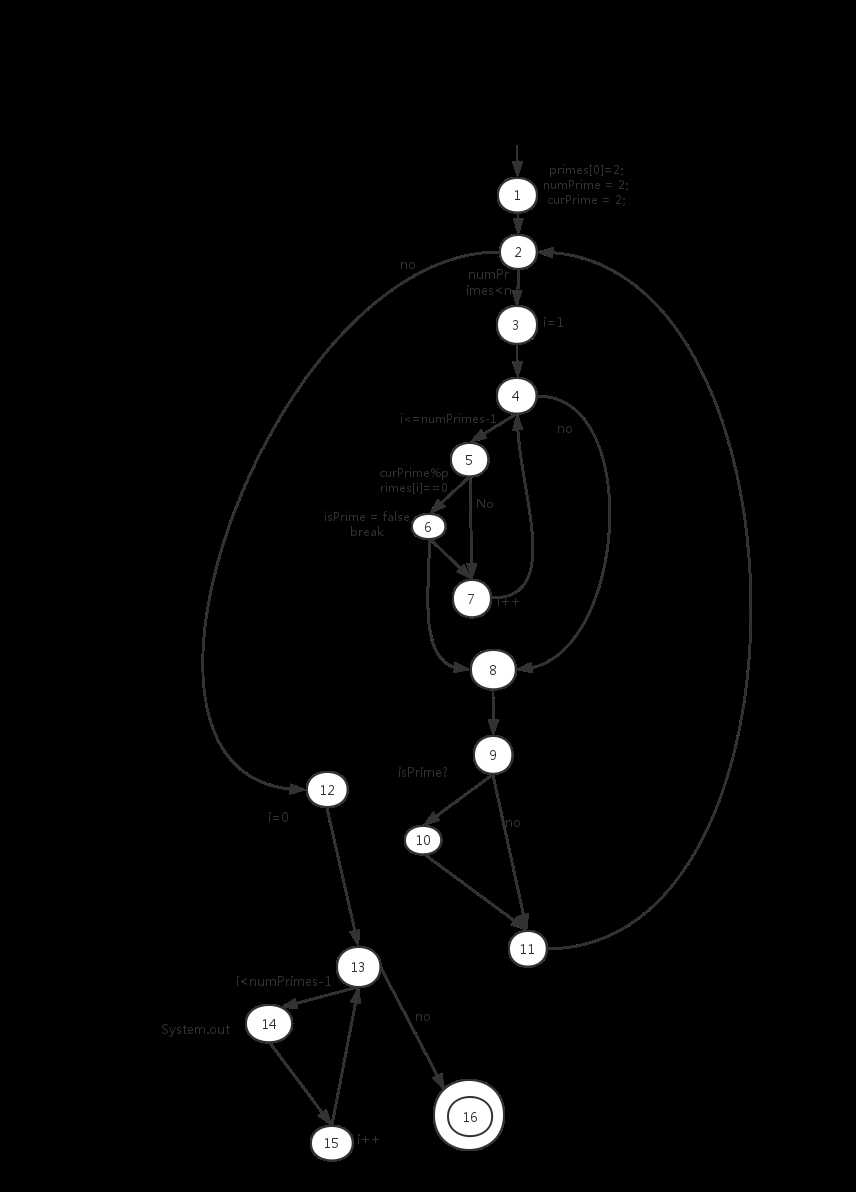
b)t1=(n=3),t2=(n=5).当数组越界时,t2更能发现问题。
c)当n=1时,程序跳过循环。
d)node coverage:{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}
edge coverage:{(1,2),(2,3),(3,4),(4,5),(5,6),(5,7),(6,7),(6,8),(7,4),(8,9),(9,10),(10,11),(9,11),(4,8),(2,12),(11,2),(12,13),(13,14),(14,15),(15,13),(13,16)}
prime path coverage:
{(1,2,3,4,5,6,7),
(1,2,3,4,5,7),
(1,2,3,4,5,6,8,9,10,11),
(1,2,3,4,8,9,10,11),
(1,2,3,4,5,6,8,9,11),
(1,2,3,4,8,9,11),
(1,2,12,13,14,15),
(1,2,12,13,16),
(2,3,4,8,9,10,11,2)
(2,3,4,8,9,11,2)
(2,3,4,5,6,8,9,10,11,2),
(2,3,4,5,6,8,9,11,2),
(4,5,7,4),
(4,5,6,7,4),
(13,14,15,13)
(15,13,14,15)}
基于Junit及Eclemma实现一个主路径覆盖的测试。
对于实验一的程序:
1 package triangle; 2 3 public class Triangle { 4 private int a,b,c; 5 6 public Triangle(int a, int b, int c) { 7 super(); 8 this.a = a; 9 this.b = b; 10 this.c = c; 11 } 12 13 public String judgeTriangle(){ 14 if(a+b>c&&a+c>b&&b+c>a){ 15 if(a==b&&a==c)return "equilLateral"; 16 else if(a==b||a==c||b==c) return "isSosceles"; 17 else return "scalene"; 18 } 19 else return "notTriangle"; 20 } 21 } 22
31 32 public class TestCase { 33 Triangle t; 34 @Test 35 public void test(){ 36 t = new Triangle(1,1,1); 37 assertEquals("equilLateral",t.judgeTriangle()); 38 t = new Triangle(1,2,2); 39 assertEquals("isSosceles",t.judgeTriangle()); 40 t = new Triangle(2,3,4); 41 assertEquals("scalene",t.judgeTriangle()); 42 t = new Triangle(1,2,3); 43 assertEquals("notTriangle",t.judgeTriangle()); 44 } 45 } 46
测试用例(1,1,1),(1,2,2),(2,3,4),(1,2,3)可完成主路径覆盖。
标签:
原文地址:http://www.cnblogs.com/tjuyyh/p/5335567.html