ST:(homework 3)Some problems about Graph Coverage

标签：

题目的源代码如下：

 1 package cn.tju.scs.printPrime;
 2 
 3 public class Prime {
 4     public static int MAXPRIMES = 30000;
 5     public static boolean isDivisible(int a,int b){
 6         int c = b%a;
 7         if (c == 0){
 8             return true;
 9         }
10         else {
11             return false;
12         }
13     }
14     public static void printPrimes(int n){
15         int curPrime;
16         int numPrimes;
17         boolean isPrime;
18         int[] primes = new int [MAXPRIMES];
19         
20         primes[0] = 2;
21         numPrimes = 1;
22         curPrime = 2;
23         while(numPrimes < n){
24             curPrime++;
25             isPrime = true;
26             for(int i = 0; i <= numPrimes - 1; i++){
27                 if(isDivisible(primes[i],curPrime)){
28                     isPrime = false;
29                     break;
30                 }
31             }
32             if(isPrime){
33                 primes[numPrimes] = curPrime;
34                 numPrimes++;
35             }
36         }
37         
38         for(int i = 0; i <= numPrimes -1; i++){
39             System.out.println("Primes: " + primes[i]);
40         }
41         
42     }
43     
44     
45 
46 }

问题：

1、以上源代码的控制流图如下：

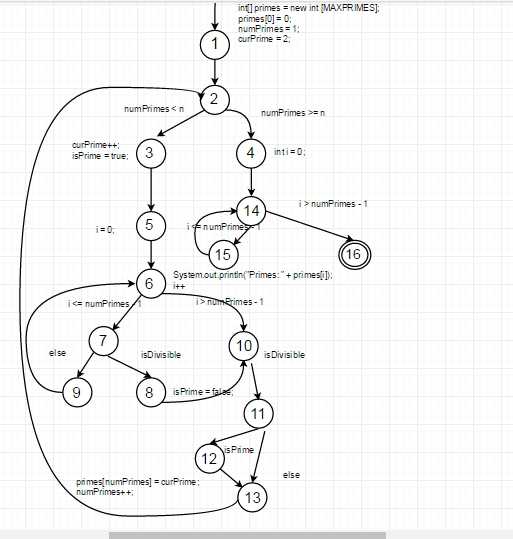
2、当把下面判断是不是素数的代码中的for的条件改成for（int i = 0; i <= 0 ; i++）是代码如下

for(int i = 0; i <= 0; i++){
　　if(isDivisible(primes[i],curPrime)){
　　isPrime = false;
　　break;
　　}
}

这样每次只判断是不是偶数，当t1 = (n = 3)时，算出的素数为2、3、5所得到的结果并没有发现错误；然而当t2 = (n = 5)时，所得的结果为2、3、5、7、9，我们能够看出所得的结果是错误的，所以能够检查出错误。所以测试用例有力相同的主路径，并不一定找出相同的错误。

3、当 n= 1时，是相应的测试路径访问连接While语句开始到for语句的边，而不通过while的循环体。

4、

节点覆盖：TR{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}

边覆盖： TR{（1,2），（2,3），（3,5），（5,6），（6,7），（7,8），（7,9），（9,6），（6,10），（8,10），（10,11），（11,12），（12,13），（11,13），（13,2），（2,4），（4,14），（14,15），（15,14），（14,16）}

主路径覆盖：TR：

　　　　　　　　　[1,2,3,5,6,7,9]

　　　　　　　　　[1,2,3,5,6,7,8,10,11,12,13]

　　　　　　　　[1,2,3,5,6,7,8,10,11,13]

　　　　　　　　　[1,2,3,5,6,10,11,12,13]

　　　　　　　　  [1,2,3,5,6,7,8,10,11,13]

　　　　　　　　   [2,3,5,6,7,8,10,11,12,13,2]

　　　　　　　　　[2,3,5,6,7,8,10,11,13,2]

　　　　　　　　　[2,3,5,6,10,11,12,13,2]

　　　　　　　　   [2,3,5,6,7,8,10,11,13,2]

　　　　　　　　   [1,2,4,14,15]

　　　　　　　　[1,2,4,14,16]

　　　　　　　　[6,7,9,6]

                          [14,15,14]

                         [3,5,6,7,8,10,11,12,13,2,4,14,15]

　　　　　　　　　[3,5,6,7,8,10,11,13,2,4,14,15]

　　　　　　　　   [3,5,6,10,11,13,2,4,14,15]

                         [3,5,6,10,11,12,13,2,4,14,15]

　　　　　　　　　[7,9,6,7,8,10,11,12,13,2,4,14,15]

　　　　　　　　　[7,9,6,7,8,10,11,13,2,4,14,15]

　　　　　　　　  [7,9,6,10,11,13,2,4,14,15]

                          [7,9,6,10,11,12,13,2,4,14,15]

　　　　　　　　  [3,5,6,7,8,10,11,12,13,2,4,14,16]

　　　　　　　　　[3,5,6,7,8,10,11,13,2,4,14,16]

　　　　　　　　  [3,5,6,10,11,13,2,4,14,16]

                       [3,5,6,10,11,12,13,2,4,14,16]

　　　　　　　　[7,9,6,7,8,10,11,12,13,2,4,14,16]

　　　　　　　　　[7,9,6,7,8,10,11,13,2,4,14,16]

　　　　　　　　  [7,9,6,10,11,13,2,4,14,16]

                          [7,9,6,10,11,12,13,2,4,14,16]

                          [15,14,16]

                          [2,3,5,6,7,8,10,11,12,13,2]

                          [3,5,6,7,8,10,11,12,13,2,3]

　　　　　　　　　 [5,6,7,8,10,11,12,13,2,3,5]

　　　　　　　　    [6,7,8,10,11,12,13,2,3,5,6]

                             [7,8,10,11,12,13,2,3,5,6,7]

                              [8,10,11,12,13,2,3,5,6,7,8]

                              [10,11,12,13,2,3,5,6,7,8,10]

  　　　　　　　    　　 [11,12,13,2,3,5,6,7,8,10,11]

　　　　　　　　  　    [12,13,2,3,5,6,7,8,10,11,12]

　　　　　　　　       [13,2,3,5,6,7,8,10,11,12,13]

                          [2,3,5,6,7,8,10,11,13,2]

　　　　　　　　　　[3,5,6,7,8,10,11,13,2,3]

                             [5,6,7,8,10,11,13,2,3,5]

　　　　　　　　　　 [6,7,8,10,11,13,2,3,5,6]

　　　　　　　　　　 [7,8,10,11,13,2,3,5,6,7]

　　　　　　　　　　 [8,10,11,13,2,3,5,6,7,8]

　　　　　　　　　　 [10,11,13,2,3,5,6,7,8,10]

　　　　　　　　　　 [11,13,2,3,5,6,7,8,10,11]

　　　　　　　　　　 [13,2,3,5,6,7,8,10,11,13]

　　　　　　　　　   [2,3,5,6,10,11,12,13,2]

　　　　　　　　      [3,5,6,10,11,12,13,2,3]

　　　　　　　　　　[5,6,10,11,12,13,2,3,5]

　　　　　　　　　　[6,10,11,12,13,2,3,5,6]

　　　　　　　　　　[10,11,12,13,2,3,5,6,10]

　　　　　　　　　　[11,12,13,2,3,5,6,10,11]

　　　　　　　　　　[12,13,2,3,5,6,10,11,12]

　　　　　　　　　　[13,2,3,5,6,10,11,12,13]

　　　　　　　　   [2,3,5,6,7,8,10,11,13,2]

　　　　　　　　　　[3,5,6,7,8,10,11,13,2,3]

　　　　　　　　　　[5,6,7,8,10,11,13,2,3,5]

　　　　　　　　　　[6,7,8,10,11,13,2,3,5,6]

　　　　　　　　　　[7,8,10,11,13,2,3,5,6,7]

　　　　　　　　　　[8,10,11,13,2,3,5,6,7,8]

　　　　　　　　　　[10,11,13,2,3,5,6,7,8,10]

　　　　　　　　　　[11,13,2,3,5,6,7,8,10,11]

　　　　　　　　　　[13,2,3,5,6,7,8,10,11,13]

　　　　　　　　　　[6,7,9,6]

　　　　　　　　　　[7,9,6,7]

　　　　　　　　　　[9,6,7,9]　　　　　　

                            [14,15,14]

　　　　　　　　　　[15,14,15]

5、测试方法的实现

 1 package cn.tju.scs.printPrime;
 2 
 3 import static org.junit.Assert.*;
 4 
 5 import org.junit.Before;
 6 import org.junit.Test;
 7 
 8 public class PrimeTest {
 9      
10     @Before
11     public void setUp() throws Exception {
12     }
13 
14     @Test
15     public void test() {
16         Prime.printPrimes(3);
17         Prime.printPrimes(4);
18         Prime.printPrimes(1);
19         Prime p = new Prime();
20     }
21 
22 }

View Code

测试效果如下图所示：

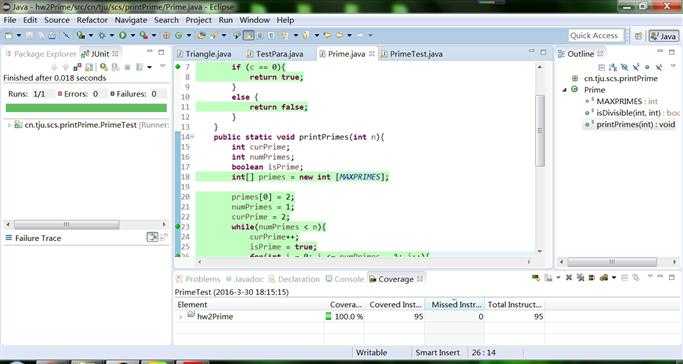
ST:(homework 3)Some problems about Graph Coverage

标签：

原文地址：http://www.cnblogs.com/superjn/p/5338277.html