标签：
关于全排列的代码在网上收集、研究了好几种，包括我自己写的也有循环实现。循环是最容易理解的，按照判定条件进行嵌套，但缺点是，如果有十个八个数据，循环嵌套的层数太深，十分臃肿。很明显，如果一段代码不够简练，我自己也不满意，肯定想尽办法解决它。所以再次记录一下全排列的递归实现。
还是按照自己的一套方法，以小见大，先不弄太多数据，在最小的范围内观察代码是如何运行的。在全排列的递归实现中，需要三个数组：
1.源数据，也就是待排的元素，比如，｛3，5，7，8....｝等等，将之放在一个数组中。
2.排好的数据。这里的排好数据是指，需要抽取几个，假如从源数据中抽取2个数据排列，这个排列的数组就定为2，因为只存放2个数据。
3.状态数组，这个数组和源数据数组等长，因为，如果有n个数据，每个数据都可能被选中，所以和源数据数组等长，整个递归过程就依靠状态数组进行工作。
代码如下：
#include <iostream> using namespace std; int a[3];/*存放排列的数组*/ int flag[3];/*状态数组*/ int b[4]={0,3,5,8};/*源数据*/ int n=3;/*源数据个数：3个*/ void f(int m) { if(m==3) /*分配完毕*/ { for(int j=1;j<3;j++)/*打印*/ cout<<a[j]; cout<<endl; } else for(int i=1;i<=n;i++) if(flag[i]==0) { a[m]=b[i]; flag[i]=1; f(m+1); flag[i]=0; } } int main() { f(1); return 0; }
现在详细分析这段代码：（所有下标都从1开始，便于分析）
为什么在代码中存在for循环，是因为，假如有n个数据，根据排列的常识，每个数据都能被选中，假如第一个元素先选中3，那么接下来的5和8具有同样的机会被选中在排列的第一个数。
第一次，m=1进入，经过循环，i=1，然后调用f(2)，这步关键是记住i这个值，它现在（停留）的位置=1.
第二次，m=2进入，经过循环，i=2，同样，这步的关键依然是i，此时（停留）的位置=2。然后调用f(3)，由于已到边界，所以打印数组，得到3，5，返回f(2)，接着，设置状态数组中的flag[i]=0，也就是把5换掉，再接着循环，取源数据的第3个数据，再递归又到边界，于是打印数组，得到3，8...
如果源数据后面还有数据，比如，9，10....等等，那么这种套路会一直持续下去，选中一个，舍弃一个，再去试下一个，如此反反复复，一直穷举到源数据的最后一个数据为止。
假如穷举完成，又退回到f(1)的时候，则它曾经选中过的所有数据都会置为0，这个容易看出来。也就是退回到f(1)的时候，状态数组就是：1 0 0。
这就说明，在确定好第一个数据之后，穷举它的下一个数据的所有可能，变成模型就是：假如要选取2个元素，最先被穷举所有可能就是它的最末位，接着往前推。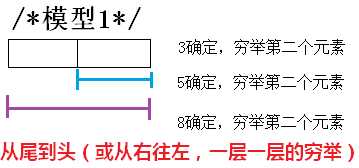
模型1就说明了这个问题，（其实很多奇怪的灵感是在写博客的时候不知不觉捕捉到的，所以写作实在很重要！）就比如这会，经过画图之后，突然就觉得这个递归和for循环极其相像！就按for循环的思路去析：
/*for循环的套路*/ for(i=1;i<=n;i++) { for(j=1;j<=n;j++) { for(....) ..... }
也就是先选取第一个元素，内部再依次嵌套内循环，再确定第二个数，第三个数...等等，区别在于，for循环是用内部的判定条件来约束，比如，第二个不等于第一个，第三个不等于第二个和第一个...所以经常有人说，递归和循环是可以相互转化的！
根据这样一分析，其实就比较明朗了，至少知道这个模型是如何工作的。现在这个例子只取两个数，把代码范围大幅度的减少，看的清楚了，如果数据很多呢，按照这种类型推理是一样的。
例如：
源数据=｛3，5，7，8，9，6｝，选取三个元素排列，根据分析，它的流程是：
最先确定第一个，第二个，然后穷举第三个，得到：3，5，7 ｜ 3，5，8｜3，5，9｜3，5，6｜，第三个穷举完毕。
再回退第二个，由于已经取了5，下一个轮到7，于是，再接着穷举第三位，得到：3，7，5｜3，7，8｜3，7，9｜....第三个穷举完毕。又回到第二个，再穷举第三个....
等到第二个穷举完全之后，又回到第一个，轮到5为第一位，接着再确定第二位，然后再穷举第三位，反反复复，依此类推，最终完成整个排列过程！
根据上面的分析，终于看出来如何在递归和循环中进行转化，先以for循环嵌套为例：
for(..) { for(...) { for(..) .. }
这是一种常见的循环嵌套，一层套一层，如何转化成为递归呢，根据上面的例子，很容易看出来，只要递归函数中有一个for循环就行，这样就把循环的嵌套压缩成一个递归形式：
void f( ) { .. for( ) { } .. }
这两者是等价的！看来基础知识掌握的还不够灵活！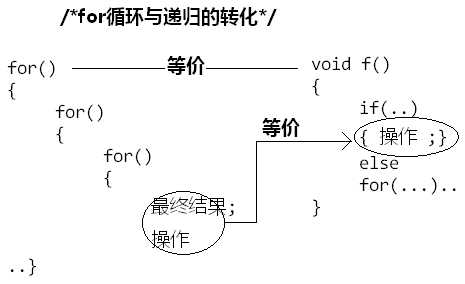
for循环的最尾端判断，在递归函数中被提到最前面。
从这个图可以看出来，原来递归只是在表面上做了一点“迷惑”，做了一点文字游戏！
这又让我想起记录的第一个小算法，九九乘法表，性质很相似，先递归分离出9，8，7，....1，然后再拿最端的1再递归，打印乘法，也就是把for循环分离出来做成递归！
我看到网上有很多代码，但很少愿意详细说明的，至少这篇日记详细的分析了它的过程！
基础知识往往看起来不太注意，但是真正理解它的思想，并且灵活运用，需要进行刻苦的演练！所以：知识无大小高低之分！
标签：
原文地址：http://www.cnblogs.com/tinaluo/p/5338929.html
