标签：des   style   blog   http   java   color   使用   os   

Interesting Fibonacci

In mathematics, the Fibonacci numbers are a sequence of numbers named after Leonardo of Pisa, known as Fibonacci (a contraction of filius Bonaccio, "son of Bonaccio"). Fibonacci‘s 1202 book Liber Abaci introduced the sequence to Western European mathematics, although the sequence had been previously described in Indian mathematics.
  The first number of the sequence is 0, the second number is 1, and each subsequent number is equal to the sum of the previous two numbers of the sequence itself, yielding the sequence 0, 1, 1, 2, 3, 5, 8, etc. In mathematical terms, it is defined by the following recurrence relation:

That is, after two starting values, each number is the sum of the two preceding numbers. The first Fibonacci numbers (sequence A000045 in OEIS), also denoted as F[n]; 
F[n] can be calculate exactly by the following two expressions:


A Fibonacci spiral created by drawing arcs connecting the opposite corners of squares in the Fibonacci tiling; this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13, 21, and 34;

So you can see how interesting the Fibonacci number is.
Now AekdyCoin denote a function G(n)

Now your task is quite easy, just help AekdyCoin to calculate the value of G (n) mod C

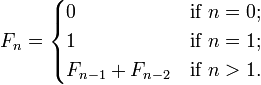
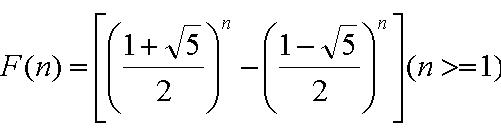
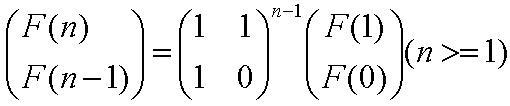
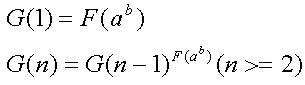
1
17 18446744073709551615 1998 139

Case 1: 120

题解及代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef unsigned long long __int65;

int f[2000];         //记录斐波那契数

int eular(int n)       //欧拉函数
{
    int cnt=n;
    for(int i=2;i*i<=n;i++)
    if(n%i==0)
    {
        cnt-=cnt/i;
        while(n%i==0)
        {
            n/=i;
        }
    }
    if(n>1)
        cnt-=cnt/n;
    return cnt;
}

int circle(int M)     //求循环节
{
    f[0]=0;
    f[1]=1;
    f[2]=1;
    for(int i=3;;i++)
    {
        f[i]=(f[i-1]+f[i-2])%M;
        if(f[i]==f[1]&&f[i-1]==f[0])
            return i-1;
    }
}

__int65 quick_mod(__int65 a,__int65 b,int M)  //快速幂取模
{
    __int65 t=1;
    a=a%M;
    while(b)
    {
        if(b&1) t=t*a%M;
        b/=2;
        a=a*a%M;
    }
    return t;
}


int main()
{
    __int65 A,B,N,C;
    int t,cas=1;
    cin>>t;
    while(t--)
    {
        cin>>A>>B>>N>>C;
        if(C==1)
        {
           printf("Case %d: 0\n",cas++);
           continue;
        }

       __int65 oula=eular(C);

       int c=circle(C);
       __int65 cl=quick_mod(A,B,c);
       cl=f[cl];

       if(oula==1)
       {
          printf("Case %d: ",cas++);
          cout<<quick_mod(cl,1,C)<<endl;
          continue;
       }

       int t=circle(oula);
       __int65 tl=quick_mod(A,B,t);
       tl=f[tl];

       __int65 mi=quick_mod(tl,N-1,oula)+oula;
       __int65 di=cl;

       printf("Case %d: ",cas++);
       cout<<quick_mod(di,mi,C)<<endl;
    }
    return 0;
}
/*
设t=a^b;G(1)=F[t];
根据递推公式G(n)=G(n-1)^F[t];可知：G(2)=F[t]^F[t];G(3)=(F[t]^F[t])^F[t]=F[t]^(F[t]*F[t]);
这样我们能看出G(n)=F[t]^(F[t]^(n-1));
首先我们在这里要先解决F[t]的值，由于a，b的值都比较大，所以求a^b是不现实的（java你可以试试）
但是我们取余的C是比较小的，所以可以使用循环节来求出F[t]%C的值，设A=F[t]%C;
接下来求A^(F[t]^(n-1))%C的值，这里还是由于F[t]的值是没有办法求的，所以需要用到取余来简化计算，
那么我们会想到费马小定理，欧拉公式，但是这里没说C是素数，所以要用到万能公式来求解，
即首先要求出φ(C),然后再求出循环节，得到F[t]%φ(C)的值，这样我们就能求解了。
注意C=1和欧拉函数值为1的情况。
*/

hdu 2814 Interesting Fibonacci,布布扣,bubuko.com

hdu 2814 Interesting Fibonacci

标签：des   style   blog   http   java   color   使用   os   

原文地址：http://blog.csdn.net/knight_kaka/article/details/38182939