标签:
1 /******************************************************* 2 * Finds and prints n prime integers 3 * Jeff Offutt, Spring 2003 4 ******************************************************/ 5 public static void printPrimes (int n) 6 { 7 int curPrime; // Value currently considered for primeness 8 int numPrimes; // Number of primes found so far. 9 boolean isPrime; // Is curPrime prime? 10 int [] primes = new int [MAXPRIMES]; // The list of prime numbers. 11 12 // Initialize 2 into the list of primes. 13 primes [0] = 2; 14 numPrimes = 1; 15 curPrime = 2; 16 while (numPrimes < n) 17 { 18 curPrime++; // next number to consider ... 19 isPrime = true; 20 for (int i = 0; i <= numPrimes-1; i++) 21 { // for each previous prime. 22 if (isDivisible(primes[i], curPrime)) 23 { // Found a divisor, curPrime is not prime. 24 isPrime = false; 25 break; // out of loop through primes. 26 } 27 } 28 if (isPrime) 29 { // save it! 30 primes[numPrimes] = curPrime; 31 numPrimes++; 32 } 33 } // End while 34 35 // Print all the primes out. 36 for (int i = 0; i <= numPrimes-1; i++) 37 { 38 System.out.println ("Prime: " + primes[i]); 39 } 40 } // end printPrimes
a. 画出函数的控制流图
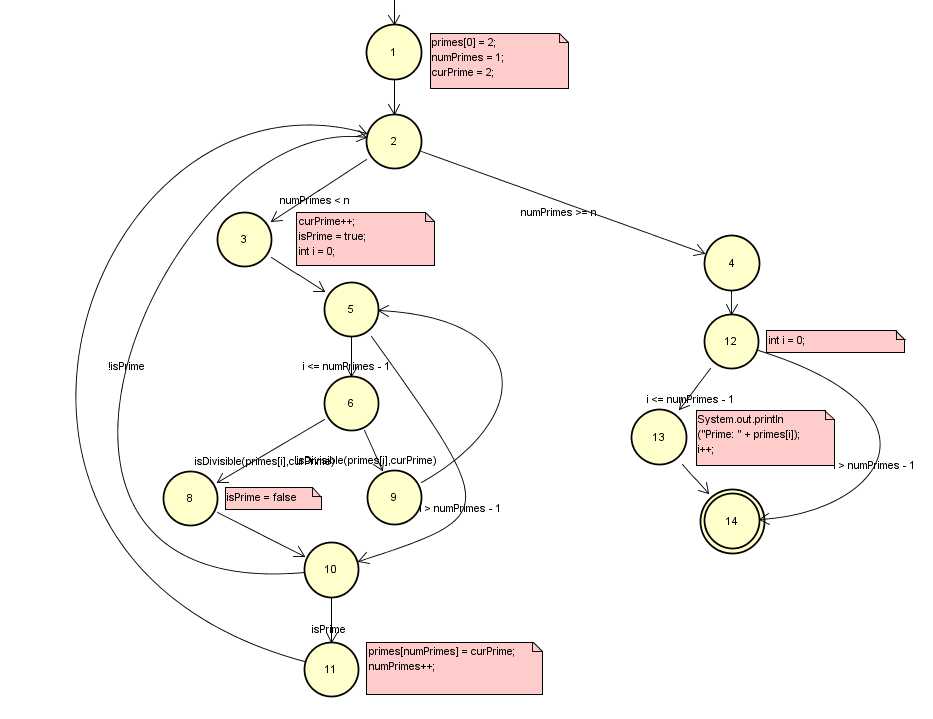
b. 设计一个t2=(n=5)能发现但t1=(n=3)不能发现的错误
如果这个函数的第22行 if (isDivisible(primes[i], curPrime))误写成了if (isDivisible(primes[0], curPrime)),即对以后的每个数是否是素数的检测,只检查它是否能被2整除。当n = 3时,找出的素数为2,3,5 没有出现错误;但是当n = 5时,找出的素数为2,3,5,7,9 出现错误
c. 寻找一组不经过while循环的测试用例
n = 1
d. 找出点覆盖、边覆盖和主路径覆盖的所有TR(测试需求)
边覆盖:[1,2,3,5,6,9,5,6,8,10,11,2,4,12,13,14]
[1,2,3,5,10,2,4,12,14]
主路径:[1,2,3,5,6,8,10,11]
[1,2,3,5,10,11]
[1,2,3,5,6,9]
[5,6,9,5]
[2,3,5,6,8,10,2]
[2,3,5,6,8,10,11,2]
[2,3,5,10,2]
[2,3,5,10,11,2]
[1,2,4,12,13,14]
[1,2,4,12,14]
[3,5,6,8,10,11,2,4,12,13,14]
[3,5,6,8,10,2,4,12,13,14]
[3,5,10,11,2,4,12,13,14]
[3,5,10,2,4,12,13,14]
[3,5,6,8,10,11,2,4,12,14]
[3,5,6,8,10,2,4,12,14]
[3,5,10,11,2,4,12,14]
[3,5,10,2,4,12,14]
[9,5,6,8,10,11,2,4,12,13,14]
[9,5,6,8,10,2,4,12,13,14]
[9,5,6,8,10,11,2,4,12,14]
[9,5,6,8,10,2,4,12,14]
主路径覆盖:
[0,1,2,3,5,6,8,10,11,2,4,12,13,14]
[0,1,2,3,5,6,8,10,11,2,4,12,14]
[0,1,2,3,5,6,8,10,2,4,12,13,14]
[0,1,2,3,5,6,8,10,2,4,12,14]
[0,1,2,3,5,6,9,5,6,8,10,11,2,4,12,13,14]
[0,1,2,3,5,6,9,5,6,8,10,2,4,12,13,14]
[0,1,2,3,5,6,9,5,6,8,10,11,2,4,12,14]
[0,1,2,3,5,6,9,5,6,8,10,2,4,12,14]
[0,1,2,3,5,10,11,2,4,12,13,14]
[0,1,2,3,5,10,2,4,12,13,14]
[0,1,2,3,5,10,11,2,4,12,14]
[0,1,2,3,5,10,2,4,12,14]
标签:
原文地址:http://www.cnblogs.com/zany/p/5339348.html