矩形波导的模式

标签：

矩形波导是使用最广泛的一种传输线。

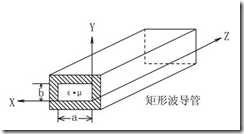
给定尺寸的波导可以传播无限多频率的电磁波，本文主要写矩形波导的场求解问题及矩形波导的相关特性。在波导内部，认为为无源空间，所以不存在传导电流和电荷，即J ＝ 0

一

对式2继续取旋度，得

同理对式1取旋度，可得到两个Helmheltz方程如下

求解的过程可总结为

每个Helmholtz方向是一个矢量方程，在矩形波导中可以分解为三个方向x\y\z的三个标题方程，从而得到波传播方向z方向的标量方程

假设E_z\H_z可分离变量，分离变量法可得到

且

代入得：

方程可以分解，所以得

其中  为截止波数，

分解后的第一个方程解为

解的第一部分是入射波，第二部分是反射波。只考虑入射波得

横向分量用纵向分量表示

整理Ex、Hy得

整理Hx、Ey得

写成矩阵形式

二 以TE波为例

分解后的第二个方程解为 

H（x,y）可分离变量，H（x,y)=X(x)Y(y)

得

一般解为：

总的解为

矩形波导的模式

标签：

原文地址：http://www.cnblogs.com/hiramlee0534/p/5339510.html