标签:blog http io 2014 for div amp 应用
最大权闭合图详细请看胡伯涛论文《最小割模型在信息学竞赛中的应用》,我在这里截图它的定义以及一些东西。
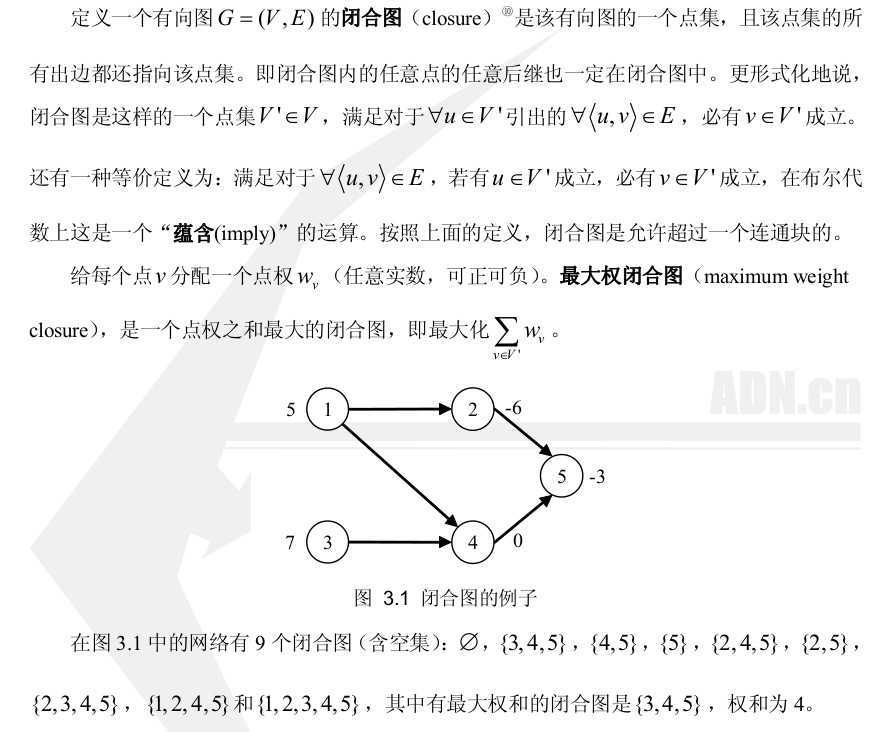

假设我们有一个图,点集的出边都是连到点集的,那么称这个为闭合图。现在这些点集都有个权值,我们要选择某个闭合图使得权值最大。
回到此题:

最大获利这一题,我们可以这样看,用户群和中转站为带权的点集,用户群的权为收益,中转站的权为负的成本,即0-成本,用户群向其中两个中转站连弧,那么这个就是一个闭合图。
我们要求这个闭合图的权值和最大,即最大收益,那么就能转移到上面的求最大权闭合图的做法去了。
做法就是:
那么此题就解决了。
(注意范围啊。,。。我又RE了一次,,好多次都是数组开小了啊>A<。)
#include <cstdio>
using namespace std;
const int N=60000, M=350000, oo=1000000000;
#define min(a,b) ((a)<(b)?(a):(b))
int ihead[N], inext[M], from[M], to[M], cap[M], cnt=1;
int cur[N], gap[N], d[N], p[N];
int isap(int s, int t, int n) {
int i, maxflow=0, f, u;
for(i=0; i<=n; ++i) cur[i]=ihead[i];
gap[0]=n; u=s;
while(d[s]<n) {
for(i=cur[u]; i; i=inext[i]) if(d[to[i]]+1==d[u] && cap[i]) break;
if(i) {
cur[u]=i; p[to[i]]=i; u=to[i];
if(u==t) {
for(f=oo; u!=s; u=from[p[u]]) f=min(f, cap[p[u]]);
for(u=t; u!=s; u=from[p[u]]) cap[p[u]]-=f, cap[p[u]^1]+=f;
maxflow+=f;
}
}
else {
if(!(--gap[d[u]])) break;
d[u]=n;
for(i=ihead[u]; i; i=inext[i]) if(cap[i] && d[u]>d[to[i]]+1)
d[u]=d[to[i]]+1, cur[u]=i;
++gap[d[u]]; if(u!=s) u=from[p[u]];
}
}
return maxflow;
}
void add(int u, int v, int c) {
inext[++cnt]=ihead[u]; ihead[u]=cnt; from[cnt]=u; to[cnt]=v; cap[cnt]=c;
inext[++cnt]=ihead[v]; ihead[v]=cnt; from[cnt]=v; to[cnt]=u; cap[cnt]=0;
}
int main() {
int n, m, sum=0;
scanf("%d%d", &n, &m);
int i, a, b, c;
for(i=1; i<=n; ++i) {
scanf("%d", &c);
add(m+i, n+m+1, c);
}
for(i=1; i<=m; ++i) {
scanf("%d%d%d", &a, &b, &c);
sum+=c;
add(i, m+a, oo); add(i, m+b, oo);
add(0, i, c);
}
printf("%d\n", sum-isap(0, n+m+1, n+m+2));
return 0;
}
最大权闭合图 && 【BZOJ】1497: [NOI2006]最大获利,布布扣,bubuko.com
最大权闭合图 && 【BZOJ】1497: [NOI2006]最大获利
标签:blog http io 2014 for div amp 应用
原文地址:http://www.cnblogs.com/iwtwiioi/p/3872099.html