标签:
一起啃PRML - 1.2 Probability Theory
@copyright 转载请注明出处 http://www.cnblogs.com/chxer/
A key concept in the field of pattern recognition is that of uncertainty.
可以看出概率论在模式识别显然是非常重要的一大块。
读其他书的时候在概率这方面就也很纠结过。
我们也还是通过一个例子来理解一下Probability Theory里面一些重要的概念。
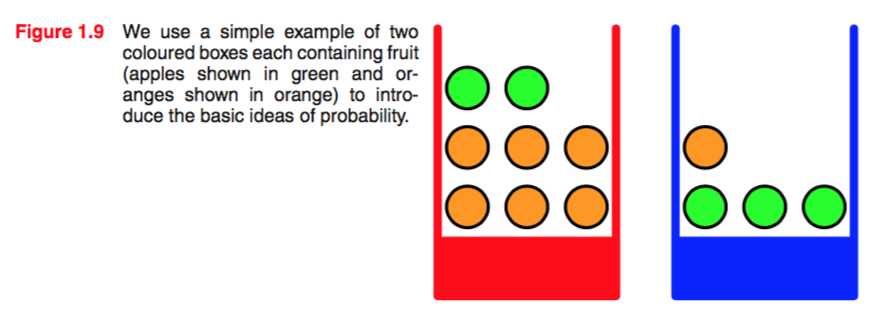
Imagine we have two boxes, one red and one blue, and in the red box we have 2 apples and 6 oranges, and in the blue box we have 3 apples and 1 orange.
绿的是苹果,黄的是橘子。
我们先假设有60%的概率选中的是蓝盒子,有40%的概率选中的是红盒子。
在讨论之前,我们还有约定一些变量:
In this example, the identity of the box that will be chosen is a random variable, which we shall denote by B. This random variable can take one of two possible values, namely r (corresponding to the red box) or b (corresponding to the blue box). Similarly, the identity of the fruit is also a random variable and will be denoted by F . It can take either of the values a (for apple) or o (for orange).
我们便有:p(B = r) = 4/10, p(B = b) = 6/10
当然了,概率一定是在[0,1]之间的数。
如果我们必须要在红色和蓝色之间做出一个选择的话,那么很显然所有的p加起来是1,这就好像把一张大饼吃完一样。
接下来我们可能就会问许许多多关于概率的问题了,当然,在此之前,我们还要学习两个工具,那就是著名的the sum rule and the product rule.
我们再来看一个例子:

这个例子就告诉我们了怎么证加法原理乘法原理
当然了证明过程无非就是推导整理
于是我们终于得到了:
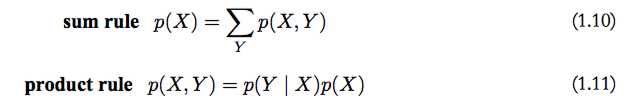
这里p(X,Y)是联合概率,可以表述为“X且Y的概率”。类似地,p(Y |X)是条件概率,可以表述为“给定X的条件下Y 的概率”,p(X)是边缘概率,可以简单地表述为“X的概率”。这两个简单的规则组成了我们在全书中使用的全部概率推导的基础。
根据乘积规则,以及对称性p(X, Y) = p(Y, X),我们立即得到了下面的两个条件概率之间的关系:
![]()
就是把两个联合概率用乘法原理展开。
最后,如果两个变量的联合分布可以分解成两个边缘分布的乘积,即p(X, Y) = p(X )p(Y), 那么我们说X和Y 相互独立(independent)。根据乘积规则,我们可以得到p(Y | X) = p(Y), 因此对于给定X的条件下的Y 的条件分布实际上独立于X的值。例如,在我们的水果盒子的例子中,如果每个盒子包含同样比例的苹果和橘子,那么p(F | B) = P (F),从而选择苹果的概率就 与选择了哪个盒子无关。
一起啃PRML - 1.2 Probability Theory
标签:
原文地址:http://www.cnblogs.com/chxer/p/5346986.html