标签:
霍夫变换——直线检测
此处膜拜大神(学到很多):http://blog.csdn.net/jia20003/article/details/7724530
这个博客更了很多图像处理算法的底层实现解析,都很详细易懂,先mark
========================我是分割线=============================
霍夫变换:CV中常用的识别几何图形的方法,其中最简单的应用就是直线检测
主要原理是对于边缘的每一个像素点(x0,y0),把可能经过它的所有直线y=kx+b,映射到k-b空间(即hough space),然后投票
但是,对于与x轴垂直的直线,斜率不存在,无法表示,所以用参数方程表示,r = x * cos(theta) + y * sin (theta), 其中(x,y)表示某一个边缘的像素点,r表示经过该点直线到原点的距离,theta表示r与x正轴的夹角。
原理分析如下图:(画得..还挺丑哈哈哈...手残)
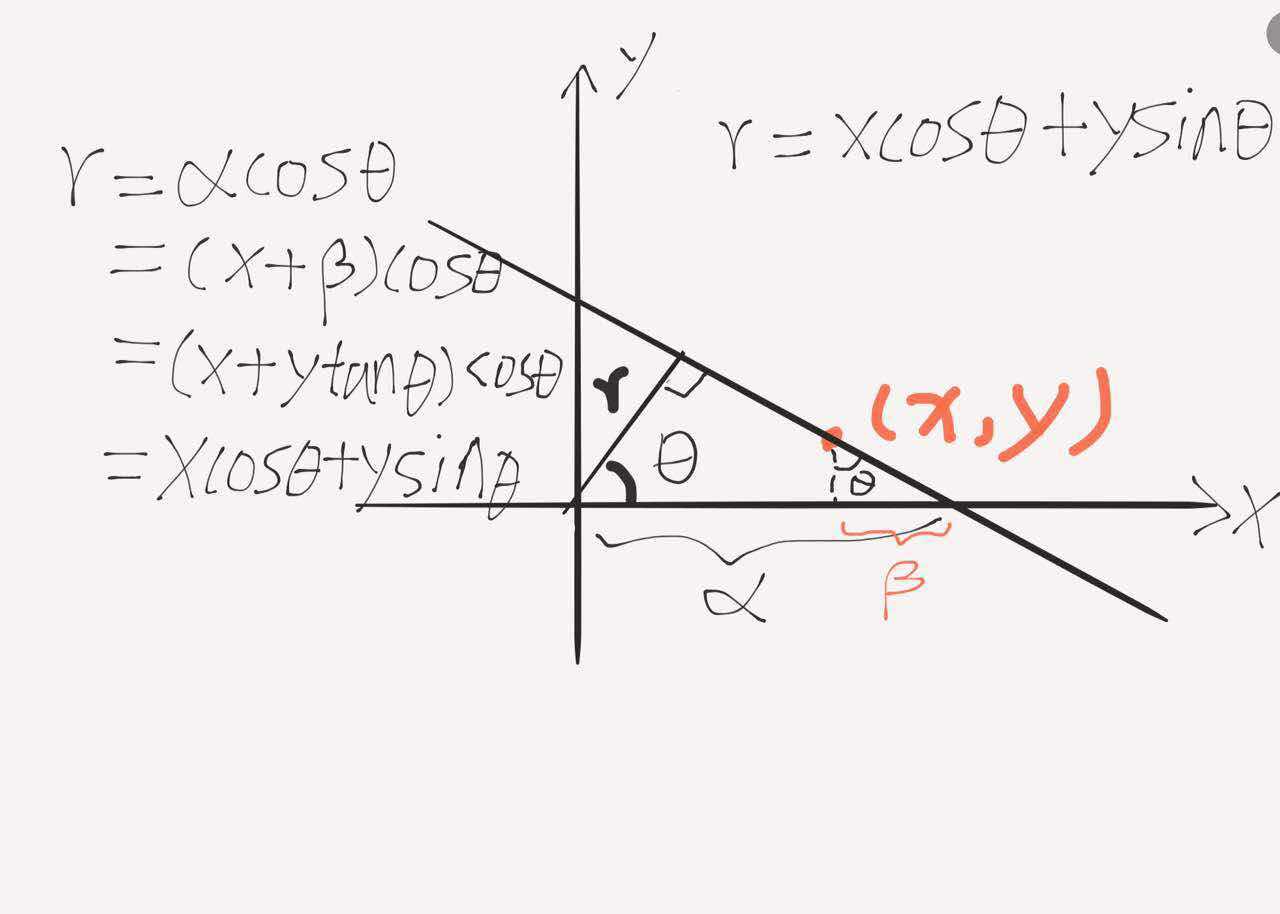

所以最终的霍夫空间可以用r-theta表示。
对于每个边缘点映射之后,在霍夫空间进行投票,每次有直线方程满足(r, theta)点,此处的像素值+1:

最后可以得到一张这样的hough-space图像:

某一个点越白(像素值越大)表示,越多的点经过这条直线,这就有可能是一条边界直线
过滤,求出局部极大值,可以得到几条直线方程(四条单像素宽直线),然后就可以根据直线方向在原图标定角点


以下为具体步骤以及实现:
1. 彩色图像RBG->灰度图Gray
(opencv上需要注意颜色空间是RGB还是BGR,CImg中RGB分别对应0,1,2通道)
2. 去噪(高斯核)
3. 边缘提取(梯度算子、拉普拉斯算子、canny; 此处实现用sobel)
4. 二值化(判断此处是否为边缘点,就看灰度值==255)
5. 映射到霍夫空间(此处准备两个容器,一个CImg用来展示hough-space概况,一个数组hough-space用来储存voting的值,因为投票过程往往有某个极大值超过255,多达几千,不能直接用灰度图来记录投票信息)
6. 取局部极大值,设定阈值,过滤干扰直线
7. 绘制直线、标定角点
实现:
1. 转灰度
可以用自带API,或者自己写
2. 高斯去噪(采用了一个标准差为1的高斯核)
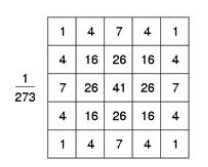
3. sobel算子提取边界
sobel时梯度算子的一种

4. 二值化(应该设置一个阈值,对不同的图,不同的阈值,以便完整显示边界)
在高斯去噪和边界提取之后都需要二值化
以下时同一张图片的二值化(阈值分别为60、80、100、127),可见,保持较好的边缘信息需要合适的阈值


5. 映射到霍夫空间
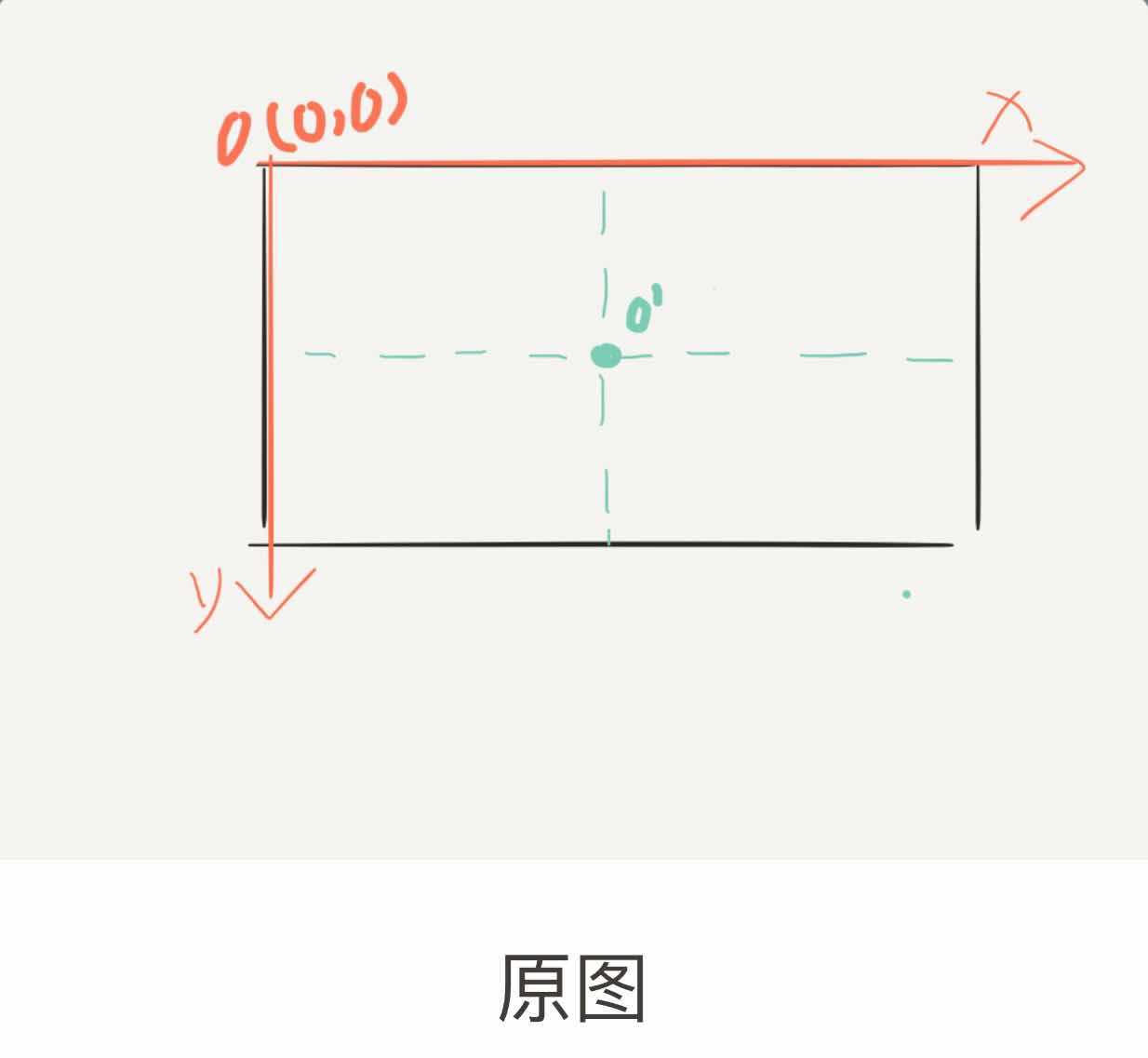
先在原图构造一个x-y平面,一一对应各点的直线方程计算O(0,0)为事实上的原点,O‘(width/2,height/2)为构造平面的原点
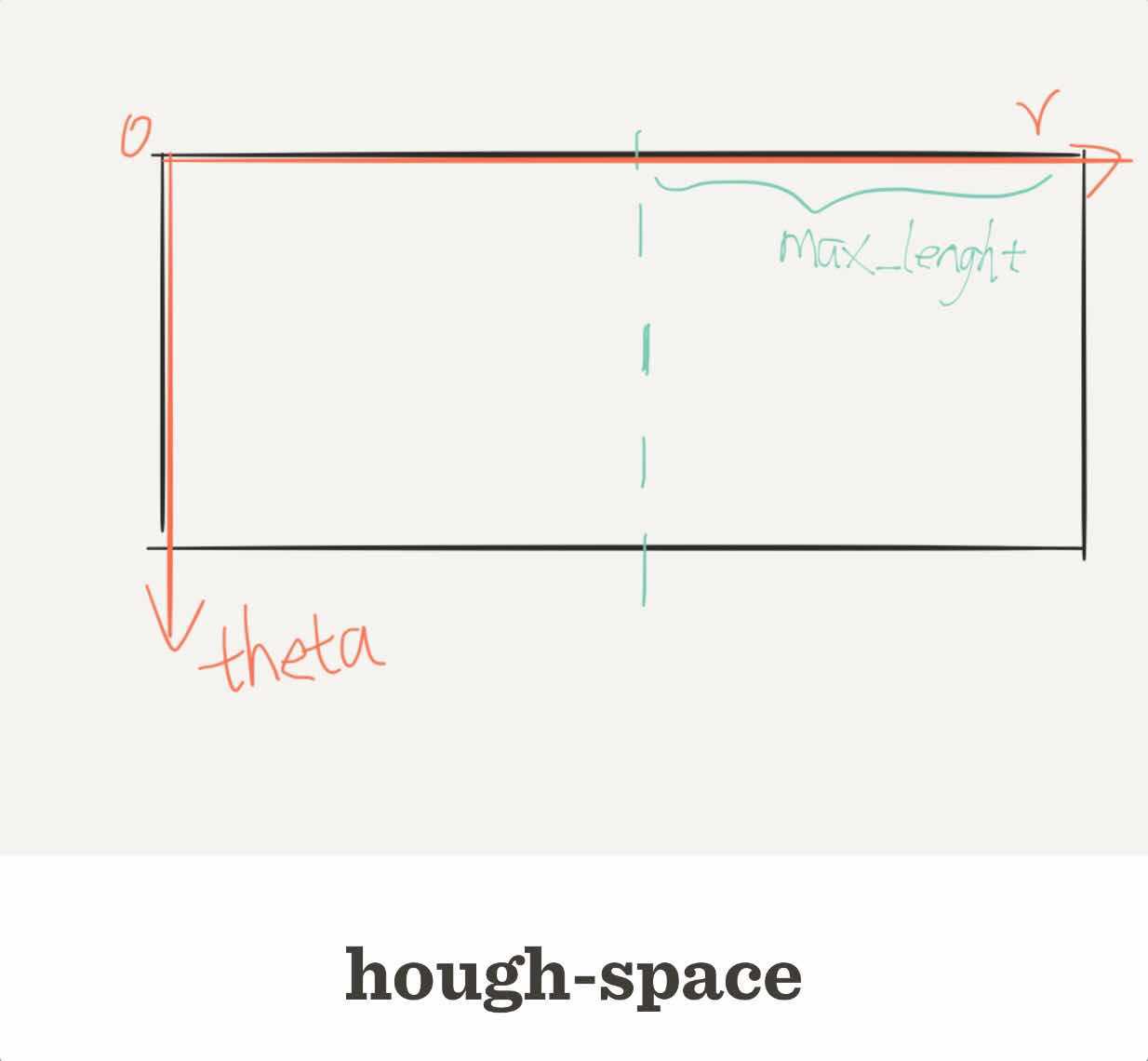
然后构造一个hough-space,其中纵轴表示theta的刻度,theta取值0~PI,分成500个刻度,r的最大值为max_length=sqrt((width/2)^2 + (height/2)^2),又r存在正负值,故而hough-space的横轴需要2*max_length
//霍夫空间,图像初始化 CImg<unsigned char> output(2 * max_length, hough_space, 1, 1); int** hough = new int*[500]; for (int k = 0; k < hough_space; k ++) hough[k] = new int[2*max_length] (); output.fill(0); //检测每一个点的所有可能直线方程,并记录投票,以及最大值 int max_hough = 0; for (int x = 0; x < width; x ++) { for (int y = 0; y < height; y ++) { int temp = (int)inputImage.atXYZC(x, y, 1, 0); if (temp == 0)continue; else { for (int degree = 0; degree < hough_space; degree ++) { double r = (x - centerX) * cos(degree * hough_intervals) + (y - centerY) * sin(degree * hough_intervals); r += max_length; if (r < 0 || (r >= 2 * max_length))continue; unsigned char temp = output.atXYZC((unsigned int)r, degree, 1, 0) + 1; output.atXYZC((unsigned int)r, degree, 1, 0) = temp; hough[degree][(int)r] ++; if (max_hough < hough[degree][(int)r])max_hough = hough[degree][(int)r]; } } } } cout << "max_hough = " << max_hough << endl;
6. 取局部极大值,设定阈值,过滤干扰直线(直线方程存储在lines中)
//输出直线轨迹 CImg<unsigned char> output1(width, height, 1, 1); output1.fill(0); //设置阈值 int threshold = int(max_hough * value); cout << "threshold = " << threshold << endl; int count = 0; vector<pair<int, int> > lines; //遍历hough空间,找到所有比阈值大的点 for (int row = 0; row < hough_space; row ++) { for (int col = 0; col < 2 * max_length; col ++) { bool newLines = true; int temp = hough[row][col]; if (hough[row][col] > threshold) { for (int k = 0; k < lines.size(); k ++) { //判断极值 if ((abs(lines[k].first - row) < 15 || abs((500 - lines[k].first) + row) < 5) && abs(lines[k].second - col) < 300) { if (hough[row][col] > hough[lines[k].first][lines[k].second]) { lines[k].first = row; lines[k].second = col; } newLines = false; } } if (newLines) { lines.push_back(make_pair(row, col)); //cout << "push " << row << " "<< col << endl; } } } }
7. 绘制直线、标定角点(角点信息存储在node中)
因为有的直线斜率K可能不存在,所以我判断两条直线相较的条件是在draw lines的时候,看一下某像素点是不是已经被标记直线,若是,则说明有直线与当前直线相交,记录交点(但是这种方法不是很好,最后讨论优缺点)
1 //角点 2 vector<pair<int, int> > node; 3 4 //draw lines 5 for (int k = 0; k < lines.size(); k ++) { 6 int row = lines[k].first; 7 int col = lines[k].second; 8 //cout << "line " << k << " = " << row << " " << col << endl; 9 double dy = sin(row * hough_intervals); 10 double dx = cos(row * hough_intervals); 11 if ((row <= hough_space / 4 ) || (row >= 3 * hough_space / 4)) { 12 for (int sRow = 0; sRow < height; ++sRow) { 13 int sCol; 14 if (row == 0 || row == 500)sCol = (int)(col - max_length) + centerX; 15 sCol = (int)((col - max_length - ((sRow - centerY) * dy)) / dx) + centerX; 16 if (sCol < width && sCol >= 0) { 17 if((int)output1.atXYZC(sCol, sRow, 1, 0) == 255)node.push_back(make_pair(sCol, sRow)); 18 else output1.atXYZC(sCol, sRow, 1, 0) = (unsigned char)255; 19 } 20 } 21 } 22 else { 23 for (int sCol= 0; sCol < width; ++sCol) { 24 int sRow; 25 if(row == 250)sRow = (int)(col - max_length) + centerY; 26 sRow = (int)((col - max_length - ((sCol - centerX) * dx)) / dy) + centerY; 27 if (sRow < height && sRow >= 0) { 28 if((int)output1.atXYZC(sCol, sRow, 1, 0) == 255)node.push_back(make_pair(sCol, sRow)); 29 else output1.atXYZC(sCol, sRow, 1, 0) = (unsigned char)255; 30 } 31 } 32 } 33 } 34 35 //在原图上标记 36 CImg<unsigned char> output2(scrImage); 37 38 //标记 39 for (int k = 0; k < lines.size(); k ++) { 40 unsigned int w = output2.width(); 41 unsigned int h = output2.height(); 42 43 int range = 50; 44 45 cout << "node x = " << node[k].first << " " << " y = " << node[k].second << endl; 46 47 for (int c = -range; c < range; c ++) { 48 for (int r = -range; r < range; r ++) { 49 int distance = (int)sqrt(c * c + r * r + 0.0); 50 if (node[k].first>= range && node[k].first < width - range && node[k].second >= range && node[k].second < height - range) { 51 if (distance <= 50 && node[k].first + c >= 0 && node[k].first + c < width && node[k].second + r >= 0 && node[k].second + r < height) { 52 output2.atXYZC(node[k].first + c, node[k].second + r, 1, 0) = (unsigned char)(255); 53 output2.atXYZC(node[k].first + c, node[k].second + r, 1, 1) = (unsigned char)(0); 54 output2.atXYZC(node[k].first + c, node[k].second + r, 1, 2) = (unsigned char)(255); 55 } 56 } 57 } 58 } 59 }
分析:
几幅图像的实验结果如下:
去噪、提取边缘、二值化之后(图1\2\3\4)




依次为图1\2\3\4的霍夫空间表示




分别为图1\2\3\4的边界直线绘制,可知四张图的边界都可以检测到




在原图上标定交点




可以发现,四张图中,只有图2的角点没有标好,其余三张图的边界直线都有斜率K不存在的情况,所以,我的标定方法适用,当直线的斜率存在时,就很可能出现一下情况:(红蓝分别表示两条直线的像素点,可以看到虽然它们相交,但是在像素表示上并无交点,这时候需要多加一个判断,是否需要用直线方程y=kx+b来直接求出交点)

标签:
原文地址:http://www.cnblogs.com/cheermyang/p/5348820.html