计算机中的进制

标签：

计算机进制(了解)

1、什么进制

进制：进制也就是进位制，是人们规定的一种进位方法。

• 对于任何一种进制---N进制，就表示某一位置上的数运算时是逢N进一位。

  举例：十进制是逢十进一，十六进制是逢十六进一，二进制就是逢二进一 。

• 计算机是信息处理的工具，任何信息必须转换成二进制形式数据后才能由计算机进行存储、运算、传输。
• 进制转换一般是由系统自动完成的，不需要我们人为转换。比如：ＰＨＰ中有专门的进制转换函数。

2、常用的进制

①二进制：有0和１两个基本数，运算规则：逢二进一。

如：(11)2表示十进制的3， 再加１,表示 (100)2　　　1010101101101010

②十进制：有0 1 2 3 4 5 6 7 8 9十个基本数，运算规则：逢十进一。

如：(19)10 再加１ (20)10

③八进制：由于二进制不方便记忆或操作，因此小型计算机引入了八进制

????有0 1 2 3 4 5 6 7八个基本数，运算规则：逢八进一。

如：(17)8 再加1 (20)8

二进制和八进制的对应关系：一个八进制数，用3位二进制来表示(R=2^3=8)

④十六进制：有0－9、A-F共16个基本数，运算规则：逢16进一。

如：(2F)16 再加1 (30)16

二进制和十六进制的对应关系：一个16进制，用4位二进制来表示（R=2^4=16

?

各种进制的对应关系表：

1. 进制的转换规则

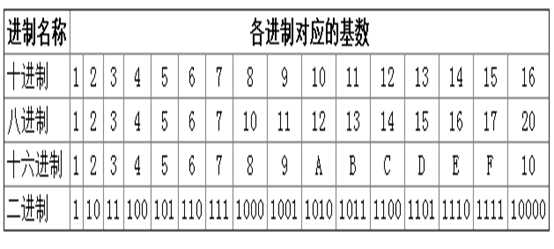
   十进制转成二进制

   1. 整数部分：除2取余法。即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。
   2. 小数部分：乘2取整法，即将小数部分乘以2，然后取整数部分，剩下的小数部分继续乘以2，然后取整数部分，剩下的小数部分又乘以2，一直取到小数部分为零为止。如果除不尽取一定的精度即可。

      二进制转成十进制

   3. 不分整数部分和小数部分
   4. 方法：按权相加法，即将二进制每位上的数乘以权(每位上的指数常数)，然后相加之和即是十进制数。
   5. 举例：将二进制（101.101）2 转成十进制
   6. 分析：1*2^2+0*2^1+1*2^0+1*2^-1+0* 2^-2 +1*2^-3=5.625(10)

   4、举例

   例如：将十进制10 .125转成二进制

   （1）整数部分：除2取余数。将整数部分每次都除以2，求(1010.001)2

   余数。一直除下去，直到商为0。读数时，从最后一位余数读起（从下往上读取）。

   

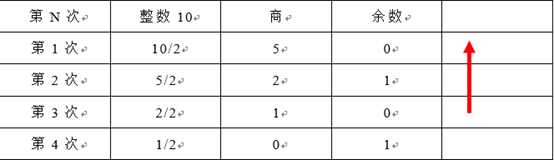
   （2）小数部分：乘2取整数。将小数部分每次乘以2，求整数。一直乘下去，直接小数部分为0。读数时，从上往下读取。

   

   ?

   ?

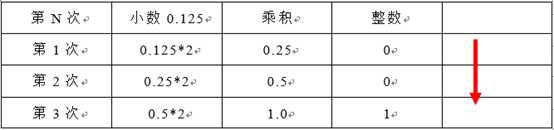
   二进制转成十进制：不分整数和小数

   转换的规则：按权相加法。将每一位上的数乘以它所在权(指数常数)，将每位的结果相加求和，和就是10进制。

   提示：小数点向左是从0开始的正指数，小数点向右是从－1开始的负指数。

   (1010.001)2 =

   1*2^3 + 0*2^2 + 1*2^1 + 0*2^0 + 0*2^-1 + 0*2^-2 + 1*2^-3

   = 8 +0 +2 +0 +0 +0+ +0.125

   = (10.125)10

计算机中的单位

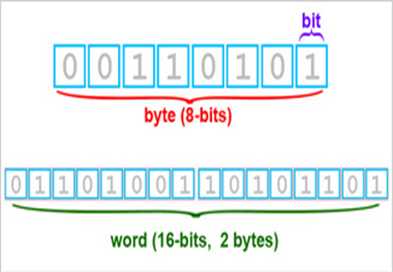
bit????（位）????????????

一个二进制数中每一个数字就是一个bit

byte（字节）????????

1byte=8bit

一个汉字占两个字节

如图：

?

计算机中的单位：

• K????????????1K = 1024byte
• M????????????1M = 1024K
• G????????????1G = 1024M
• T????????????1T = 1024G

计算机中的进制

标签：

原文地址：http://www.cnblogs.com/nyxd/p/5352331.html