哈夫曼树

标签：

1.构造哈夫曼树的方法 
对于已知的一组叶子的权值Ｗ 1 ，Ｗ 2...... ，Ｗ n 
①首先把 n 个叶子结点看做 n 棵树（仅有一个结点的二叉树），把它们看做一个森林。 
②在森林中把权值最小和次小的两棵树合并成一棵树，该树根结点的权值是两棵子树权值之和。这时森林中还有 n-1 棵树。 
③重复第②步直到森林中只有一棵为止，此树就是哈夫曼树。

现给一组 (n=4) 具体的权值: 2 ， 4 ， 5 ， 8 ，下边是构造具体过程：

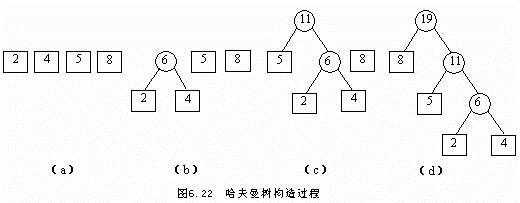
n 个叶子构成的哈夫曼树其带权路径长度是唯一的，但树形是不唯一的。因为将森林中两棵权值最小和次小的子棵合并时，哪棵做左子树，哪棵做右子树并不严格限制。

2.poj3253

  sum=合并两个数的代价就是两个数的和；

最终合并成一个数的总代价最小

故，每次去最小的两个，合并，加入数列；

3代码

#include<iostream>
#include<algorithm>
using namespace std;
int a[30000];
int main()
{
    int n;
    int i,j,k,t=1;
    long long  ans=0;
    cin>>n;
    for (i=1;i<=n;i++)
        cin>>a[i];
    sort(a+1,a+1+n);
   for (i=1;i<=n-1;i++)
   {
       int flag=0;
       int sum=a[i]+a[i+1];
       for (j=i+1;j<=n;j++)
         if(sum<=a[j+1])
       {
           a[j]=sum;
           flag=1;
           break;
       }
       else a[j]=a[j+1];
       if(flag==0) a[n]=sum;
       ans+=sum;
   }
    cout<<ans<<endl;
    return 0;
}

哈夫曼树

标签：

原文地址：http://www.cnblogs.com/dlut-li/p/5361036.html