标签:
1、概念:
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,因此有时需要离散化让空间压缩。
2、基本操作:
(1)线段树的构造
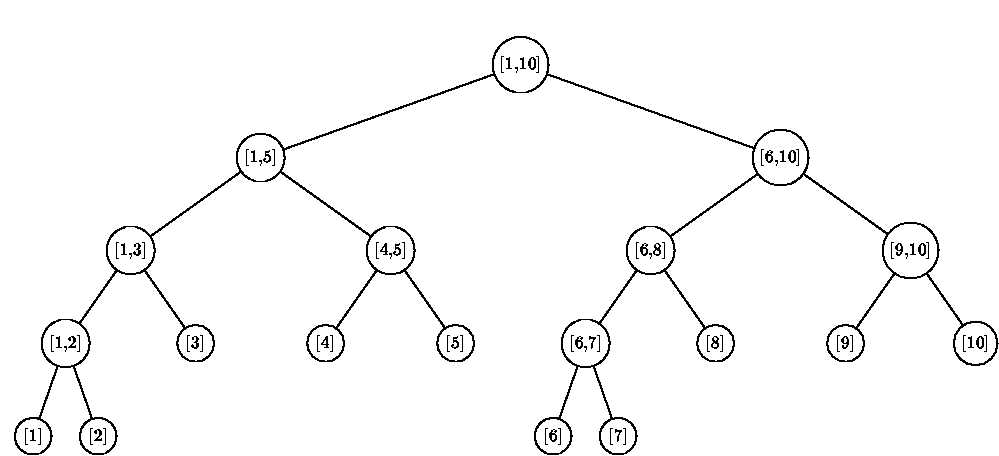
让根节点表示区间[0,N-1],即所有N个数所组成的一个区间,然后,把区间分成两半,分别由左右子树表示。不难证明,这样的线段树的节点数只有2N-1个,是O(N)级别的。
伪代码如下(递归过程):
function 构造以v为根的子树 if v所表示的区间内只有一个元素 v区间的最小值就是这个元素, 构造过程结束 end if 把v所属的区间一分为二,用w和x两个节点表示。 标记v的左儿子是w,右儿子是x 分别构造以w和以x为根的子树(递归) v区间的最小值 <- min(w区间的最小值,x区间的最小值) end functionNode *build(int l , int r ) //建立二叉树 { Node *root = new Node; root->left = l; root->right = r; //设置结点区间 root->leftchild = NULL; root->rightchild = NULL; if ( l +1< r ) { int mid = (r+l) >>1; root->leftchild = build ( l , mid ) ; root->rightchild = build ( mid , r) ; } return root; }
(2)线段树中的线段插入
增加一个cover的域来计算一条线段被覆盖的次数,因此在建立二叉树的时候应顺便把cover置0。
插入一条线段[c,d]:
void Insert(int c, int d , Node *root ) { if(c<= root->left&&d>= root->right) root-> cover++; else { if(c < (root->left+ root->right)/2 ) Insert (c,d, root->leftchild ); if(d > (root->left+ root->right)/2 ) Insert (c,d, root->rightchild ); } }
(3)线段树的线段删除
删除一条线段[c,d]:
void Delete (int c , int d , Node *root ) { if(c<= root->left&&d>= root->right) root-> cover= root-> cover-1; else { if(c < (root->left+ root->right)/2 ) Delete ( c,d, root->leftchild ); if(d > (root->left+ root->right)/2 ) Delete ( c,d, root->rightchild ); } }
参考博客:http://blog.csdn.net/metalseed/article/details/8039326
标签:
原文地址:http://www.cnblogs.com/darklights/p/5361404.html