标签：
作者：樱花猪
本文为七月算法（julyedu.com）12月机器学习第六次次课在线笔记。本节课主要介绍了一种在机器学习需要经常使用到的计算方法——梯度下降法并在最后提出了另一种下降法的思路——拟牛顿法。梯度下降法是一个连接理论和计算机计算的桥梁，这种方法通过迭代来逐步完成对于目标函数的演化，将离散和连续有机的结合起来。实际上梯度下降法在许多有关偏微分方程算法中也有所用到，例如水平集、主动轮廓模型等。通过本次课程的学习，我们能够更加具体和感性的理解梯度下降，从书本的理论中走出来。
引言：
由于有头几次数学课程的铺垫，实际上机器学习算法在公式推导上几乎没有太多的难点，接下来的课程相对也比较的轻松。只是初次接触机器学习不太能够直观的想象的机器是怎么通过计算慢慢的得到最后的结果。好在邹博为我们提供了大量简单易懂的代码和形象生动的配图。而个人认为机器学习需要解决的问题在于如何建立算法产生的思路和各种算法之间的联系。
本次课程接着上次回归课程中提到的有关于梯度下降的内容继续讲，主要分享了上次没有仔细讲解的调整学习率问题，并在最后提出了另一种下降方法拟牛顿法。本次课程理论内容不太多，需要在日后的实践中加强理论的理解。
预备知识
高等数学
矩阵求导
梯度下降法
梯度下降回顾；优化学习率；
拟牛顿
牛顿法；拟牛顿法；BFGS;L-BFGS;
一、梯度下降法
注：机器学习中向量没有事先给出是行向量还是列向量，默认就是列向量。
1、梯度下降算法回顾
具体方法：
a. 初始化
（随机初始化）
b. 迭代，新的
能够使得更小
c. 如果
能够继续减少，返回b
；其中，
需要解决和优化的问题：
a. 参数更新时机：
传统方法；批量梯度下降法；折中mini-batch法；随机梯度下降法SGD；
b. 如何确定学习率
使用固定学习率还是变化学习率
固定学习率存在的问题：有些情况下降不下去了
学习率设置多大比较好？
C、下降方向
处理梯度方向，其他方向是否可以？
可行方向和梯度方向有何关系？
2、优化学习率
基本思路：
在斜率(方向导数)大的地方，使用小学习率。
在斜率(方向导数)小的地方，使用大学习率。
3、学习率的计算标准
把学习率看作是变量，样本点x,y都是已知的。
a. 因为梯度下降是寻找f(x)的最小值，那么，在
和
（下降方向）给定的前提下，即寻找函数
的最小值。即：
b. 如果
可导，局部最小值
处的满足：
c. 将
带入，则有：
d. 下降方向
可以选择负梯度方向
（或者选择与负梯度夹角小于90°的某方），从而：
f. 则必存在某
，使得
，这里
即为要寻找的学习率。
4、线性搜索
4.1 二分线性搜索(Bisection Line Search) ：
不断将区间
分成两半，选择端点异号的一侧，知道区间足够小或者找到当前最优学习率。
4.2 回溯线性搜索(Backing Line Search) ：
基于Armijo准则计算搜素方向上的最大步长。其基本思想是沿着搜索方向移动一个较 大的步长估计值，然后以迭代形式不断缩减步长，直到该步长使得函数值
相对与当前函数值
的减小程度大于预设的期望值(即满足Armijo准则)为止。
附：Armijo准则，Armijo条件是一种一维搜索的停止条件，不精确的一维搜索条件规定迭代步长首先应该保证使目标函数充分减小，这个条件使用以下不等式描述：
4.3比较：
二分线性搜索的目标是求得满足的 
最优步长近似值，而回溯线性搜索放松了对步长的约束，只要步长能使函数值有足够大的变化即可。
二分线性搜索可以减少下降次数，但在计算最优步长上花费了不少代价；回溯线性搜索找到一个差不多的步长即可。
4.4回溯法改进：插值法
采用多项式插值法(Interpolation) 拟合简单函数，然后根据该简单函数估计函数的极值点，这样选择合适步长的效率会高很多。
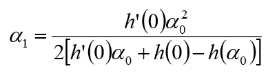（二次差值）
其中，
为本次最优值，
为上一次尝试迭代步长。
若
满足Armijo准则，则输出该学习率；否则，继续迭代。
注：更高次的差值会影响计算速度。
二、拟牛顿
1、牛顿法
提出：修改搜索方向，不仅仅说是梯度下降。
尝试：方向为一阶导和二阶导相除
二阶导数反应了函数的凸凹性；二阶导越大，一阶导的变化越大；利用二阶导做修正。
推广：牛顿法，将上述方法推广到多维，用方向导数代替一阶导，用Hessian矩阵代替二阶导。
2、拟牛顿
提出：求Hessian矩阵的逆影响算法效率，同时搜索方向只要和负梯度的夹角小于90°即可， 因此，可以用近似矩阵代替Hessian矩阵，只要满足该矩阵正定、容易求逆，或者可以通过若干步递推公式计算得到。
修正方案：
BFGS / LBFGS
n Broyden–Fletcher –Goldfarb -Shanno
L-BFGS
BFGS需要存储n×n的方阵
用于近似 Hessian阵的逆矩阵；而L-BFGS仅需要存储 最近m(m约为10，m=20足够)个 用于近似Ck即可。
L-BFGS的空间复杂度O(mn)，若将m看做常 数，则为线性，特别适用于变量非常多的优 化问题。
标签：
原文地址：http://www.cnblogs.com/Dr-XLJ/p/5367114.html
