hihoCoder #1142 : 三分求极值

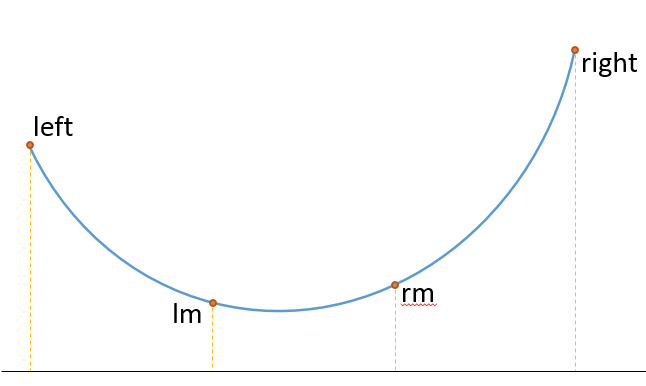
对于计算机编程来说是非常麻烦的一件事。
进一步观察题目，我们能够发现依据带入的X值不同，d的长度恰好满足凸形函数。而我们要求的最短距离d，正好就是这个凸形函数的极值。那么三分法不就正好能够用来解决这道题目了么？须要注意在解题过程中一定要想清楚怎样划分区间，我们求的各个变量究竟是什么含义。

 代码：

#include <bits/stdc++.h>
using namespace std;
const double MIN=-1e3;
const double MAX=1e3;
const double eps=1e-6;
double a,b,c,x,y;
double Calc(double X)
{
    return sqrt((X-x)*(X-x)+(a*X*X+b*X+c-y)*(a*X*X+b*X+c-y));
}
void solve()
{
    double left=MIN,right=MAX;
    double mid,midmid;
    double mid_value,midmid_value;
    while(left+eps<right)
    {
        mid=(left+right)/2;
        midmid=(mid+right)/2;
        mid_value=Calc(mid);
        midmid_value=Calc(midmid);
        if(mid_value<=midmid_value) right=midmid;
        else left=mid;
    }
    printf("%.3f\n",Calc(left));
}
int main()
{
    scanf("%lf%lf%lf%lf%lf",&a,&b,&c,&x,&y);
    solve();
}